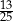/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 4139450

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest pięcioelementowy zbiór 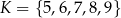K = {5,6,7,8 ,9 } . Wylosowanie każdej liczby z tego zbioru jest jednakowo prawdopodobne. Ze zbioru 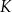K losujemy ze zwracaniem kolejno dwa razy po jednej liczbie i zapisujemy je w kolejności losowania. Oblicz prawdopodobieństwo zdarzenia 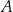A polegającego na tym, że suma wylosowanych liczb jest liczbą parzystą.

Rozwiązanie

Każdą liczbę możemy wybrać na 5 sposobów, więc

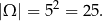
|Ω | = 52 = 2 5.

Sposób I

W zdarzeniach sprzyjających albo obie liczby są parzyste – są

2⋅ 2 = 4

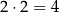
takie zdarzenia, albo obie są nieparzyste – jest

3⋅ 3 = 9

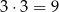
takich zdarzeń. Interesujące nas prawdopodobieństwo jest więc równe

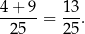
4-+-9-= 13. 25 25

Sposób II

Wypisujemy wszystkie zdarzenia sprzyjające

55, 7 7, 99, 57, 75, 59, 9 5, 79 , 97 66, 8 8, 68, 86.

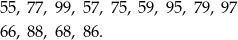
Jest więc 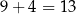9 + 4 = 1 3 zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe

13. 25

 
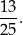
Odpowiedź: 1235

Wersja PDF