/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 6462700

Ze zbioru 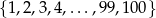{1,2,3,4,...,99,1 00} wybieramy cztery różne liczby i obliczamy ich sumę. Oblicz jakie jest prawdopodobieństwo tego, że suma wybranych liczb jest nieparzysta. Wynik podaj w postaci ułamka nieskracalnego.

Wersja PDF

Rozwiązanie

Wszystkich możliwości wyboru czterech liczb z danego zbioru jest

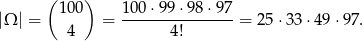
(10 0) 100 ⋅99 ⋅98 ⋅97 |Ω | = = ----------------= 2 5⋅33 ⋅49 ⋅97. 4 4!

Jeżeli suma wybranych liczb ma być nieparzysta, to musimy wybrać trzy liczby parzyste i jedną nieparzystą lub jedną liczbę parzystą i 3 nieparzyste. Obliczmy ile jest możliwości takich wyborów.

Trzy liczby parzyste możemy wybrać na

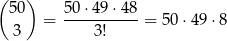
( ) 50 50 ⋅49 ⋅48 = -----------= 50 ⋅49⋅ 8 3 3 !

sposobów. Do tego musimy dobrać jedną liczbę nieparzystą – możemy to zrobić na 50 sposobów. W tym przypadku mamy więc

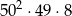
2 50 ⋅49 ⋅8

możliwości.

Zauważmy, że dokładnie tyle samo jest możliwości wyboru czterech liczb, wśród których są trzy nieparzyste i jedna parzysta – jest tak, bo w danym zbiorze jest dokładnie tyle samo liczby parzystych i nieparzystych. Interesujące nas prawdopodobieństwo jest więc równe

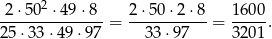
2 ⋅502 ⋅49 ⋅8 2 ⋅50 ⋅2⋅ 8 16 00 --------------= ----------- = -----. 25⋅3 3⋅49 ⋅97 33 ⋅97 32 01

 
Odpowiedź: 13620001

Wersja PDF