/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 6974931

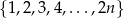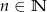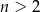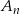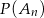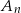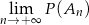Ze zbioru liczb: { 1,2,3,4,...,2n } , gdzie n ∈ N i n > 2 losujemy kolejno trzy razy po jednej liczbie bez zwracania. Niech An oznacza zdarzenie: iloczyn wylosowanych liczb jest liczbą nieparzystą, a P (An ) prawdopodobieństwo zajścia zdarzenia An . Oblicz: lim P(An ) n→ + ∞ .

Wersja PDF

Rozwiązanie

Trzy liczby z podanego zbioru można wylosować na

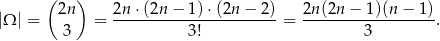
( 2n) 2n ⋅ (2n− 1)⋅ (2n − 2) 2n(2n − 1)(n − 1 ) |Ω | = = ----------------------- = ------------------. 3 3! 3

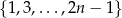W podanym zbiorze jest n liczb nieparzystych: {1,3,...,2n − 1 } . Jeżeli iloczyn wylosowanych liczb ma być nieparzysty, to wszystkie muszą być nieparzyste, więc jest

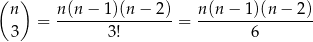
(n ) n (n− 1)(n − 2) n(n − 1)(n − 2 ) = ---------------- = ---------------- 3 3! 6

zdarzeń sprzyjających i interesujące nas prawdopodobieństwo jest równe

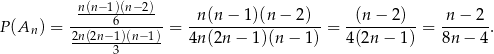
n(n− 1)(n− 2) ------6------ -n(n-−--1)(n−--2)-- -(n-−-2)-- n-−--2- P(An ) = 2n(2n−-1)(n−-1)-= 4n(2n − 1)(n − 1) = 4(2n − 1) = 8n − 4. 3

Mamy zatem

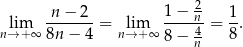
n − 2 1− 2n 1 nl→im+∞ -------= n→lim+ ∞ ----4-= -. 8n− 4 8− n 8

 
Odpowiedź: 1 8

Wersja PDF