/Szkoła średnia/Prawdopodobieństwo/Z definicji/Zbiory liczb/Parzystość

Zadanie nr 8594132

Ze zbioru 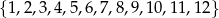{1,2,3,4,5,6,7 ,8 ,9,10,11,12} losujemy podzbiór trójelementowy. Jakie jest prawdopodobieństwo, że iloczyn liczb będących elementami wylosowanego podzbioru jest liczbą parzystą?

Wersja PDF

Rozwiązanie

Zdarzeń elementarnych jest:

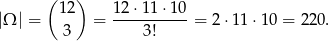
( 12) 12 ⋅11 ⋅10 |Ω | = = -----------= 2⋅11 ⋅10 = 220. 3 3!

Sposób I

Są trzy rodzaje zdarzeń sprzyjających.

Mogą być trzy liczby parzyste. Trzy liczby parzyste wybieramy ze zbioru 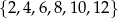{2 ,4,6,8,10,12} . Możemy to więc zrobić na

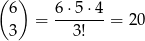
( ) 6 = 6⋅-5⋅4-= 20 3 3!

sposobów.

Jeżeli są dokładnie dwie liczby parzyste, to musimy do nich dobrać jedną liczbę nieparzystą ze zbioru 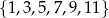{1,3,5 ,7,9,11} . Jest więc

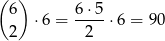
( ) 6 6 ⋅5 2 ⋅ 6 = --2- ⋅6 = 90

zdarzeń tego typu.

Ostatnia możliwość, to jedna liczba parzysta i dwie liczby nieparzyste. Takich zdarzeń jest

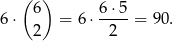
( ) 6 ⋅ 6 = 6⋅ 6⋅5-= 90. 2 2

Prawdopodobieństwo jest więc równe

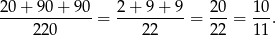
20-+-90-+-9-0 2-+-9-+-9- 20- 10- 220 = 22 = 22 = 11.

Sposób II

Tym razem zajmijmy się zdarzeniem przeciwnym. W zdarzeniu takim musimy wylosować trzy liczby nieparzyste. Możemy to zrobić na

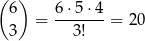
( ) 6 = 6⋅-5⋅4-= 20 3 3!

sposobów. Interesujące nas prawdopodobieństwo jest więc równe

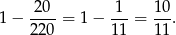
1− -20-= 1− -1-= 10. 220 11 11

 
Odpowiedź: 1101

Wersja PDF