Zadanie nr 9349844
Ze zbioru liczb 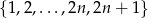 ,
, 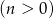 , losujemy jednocześnie dwie liczby. Niech
, losujemy jednocześnie dwie liczby. Niech 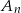 oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.
oznacza zdarzenie: iloczyn wylosowanych liczb będzie liczbą parzystą. Wyznacz prawdopodobieństwo tego zdarzenia.
Rozwiązanie
Dwie liczby z podanego zbioru można wylosować na
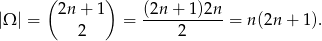
W podanym zbiorze jest  liczb parzystych (
liczb parzystych (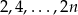 ) oraz
) oraz 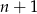 liczb nieparzystych (
liczb nieparzystych (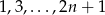 ).
).
Sposób I
Mamy dwa rodzaje zdarzeń sprzyjających: możemy wylosować dwie liczby parzyste, lub jedną parzystą i jedną nieparzystą. Dwie liczby parzyste możemy wylosować na
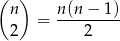
sposobów, a jedną parzystą i jedną nieparzystą na
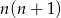
sposobów. Zatem szukane prawdopodobieństwo jest równe
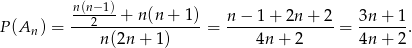
Sposób II
Mogliśmy też łatwo policzyć prawdopodobieństwo zdarzenia przeciwnego, czyli prawdopodobieństwo wylosowania pary liczby, których iloczyn jest nieparzysty. Aby tak było, obie liczby muszą być nieparzyste, co może się zdarzyć na
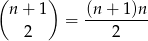
sposobów. Zatem
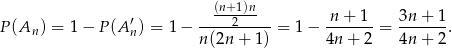
Odpowiedź: