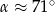/Szkoła średnia/Geometria/Stereometria/Czworościan foremny

Zadanie nr 2444423

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz cosinus kąta jaki tworzą dwie ściany czworościanu foremnego. Podaj przybliżoną miarę tego kąta.

Rozwiązanie

Zaczynamy od rysunku.

PIC

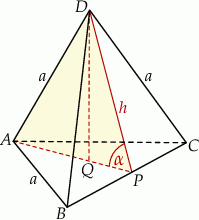
Ponieważ płaszczyzna 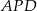AP D , przechodząca przez krawędź 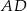AD i środek krawędzi 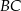BC jest prostopadła do krawędzi 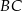BC , kąt o którym mowa w treści zadania to dokładnie kąt 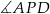∡AP D . Jego cosinus możemy łatwo obliczyć z trójkąta prostokątnego 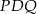PDQ , gdzie 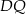DQ jest wysokością czworościanu. Ponieważ punkt 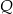Q jest środkiem trójkąta 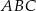ABC , dzieli on odcinek 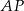AP w stosunku 2:1, czyli

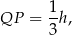
QP = 1h, 3

gdzie 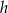h to wysokość trójkąta równobocznego 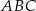ABC . Ponadto 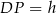DP = h , czyli

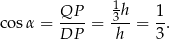
1 QP-- 3h- 1- co sα = DP = h = 3.

Z tablic odczytujemy, że 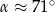α ≈ 71 ∘ .  
Odpowiedź: 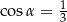cosα = 1 3 , α ≈ 71∘

Wersja PDF