/Szkoła średnia/Geometria/Stereometria/Czworościan foremny

Zadanie nr 5669484

Dodaj do ulubionych
Dodaj do rozwiązanych

Oblicz promień kuli stycznej do wszystkich krawędzi czworościanu foremnego o krawędzi długości a .

Rozwiązanie

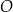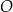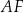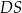Niech O będzie środkiem czworościanu (tzn. O jest punktem przecięcia się wysokości AF i DS czworościanu).

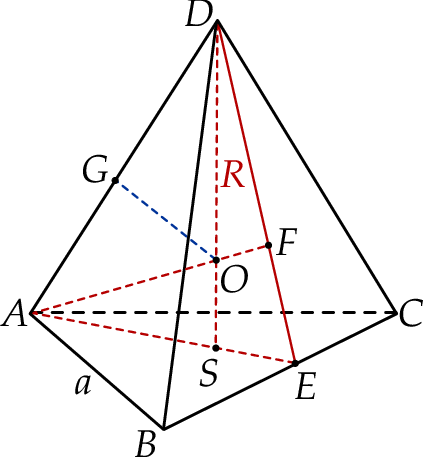
ZINFO-FIGURE

Ze względu na symetrię czworościanu foremnego (z każdej strony wygląda tak samo), odległość punktu 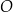O od wszystkich wierzchołków czworościanu jest taka sama (jest to środek sfery opisanej na czworościanie). To oznacza, że wszystkie trójkąty, których wierzchołkami są dwa wierzchołki czworościanu i punkt 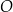O (czyli trójkąty 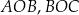AOB ,BOC , itd.) są przystające. To z kolei oznacza, że odległość punktu 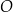O od każdej krawędzi czworościanu jest taka sama, czyli punkt 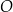O jest środkiem interesującej nas kuli stycznej do wszystkich krawędzi czworościanu.

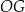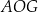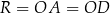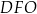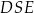Interesujący nas promień OG kuli stycznej do krawędzi czworościanu obliczymy z trójkąta prostokątnego AOG , ale do tego potrzebujemy obliczyć długość promienia R = OA = OD promienia sfery opisanej na czworościanie. To z kolei zrobimy z podobieństwa trójkątów DF O i DSE . Zatem do dzieła.

Obliczamy najpierw długość wysokości czworościanu

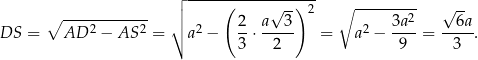
┌│ -----(---------)-- ∘ --------- -- ∘ ------------ │ 2 a√ 3 2 3a2 √ 6a DS = AD 2 − AS 2 = ∘ a2 − --⋅----- = a2 − ----= ----. 3 2 9 3

Teraz korzystamy z podobieństwa trójkątów prostokątnych 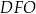DF O i DSE .

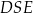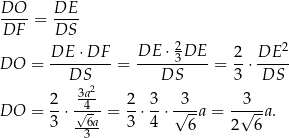
DO-- DE-- DF = DS 2 2 DO = DE--⋅DF--= DE--⋅3DE--= 2-⋅ DE-- DS DS 3 DS 2 3a2- 2 3 3 3 DO = --⋅√-4- = --⋅ --⋅√--a = -√--a. 3 --63a 3 4 6 2 6

Pozostało teraz skorzystać z twierdzenia Pitagorasa w trójkącie 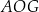AOG .

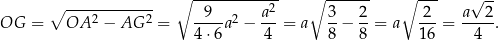
------------ ∘ ------------ ∘ 9 a2 ∘ -3---2 ∘ -2- a√ 2- OG = OA 2 − AG 2 = ----a 2 − --= a -− --= a ---= -----. 4 ⋅6 4 8 8 16 4

 
Odpowiedź: √ - a--2 4

Wersja PDF