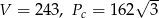Zadanie nr 7792329

Wysokość czworościanu foremnego ma długość 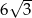√ -- 6 3 . Oblicz jego objętość i pole powierzchni całkowitej.

Rozwiązanie

Zaczynamy od rysunku.

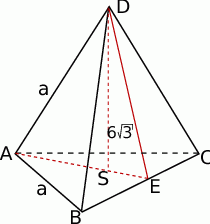
Zaczniemy od wyliczenia długości krawędzi czworościanu. Ze wzoru na wysokość w trójkącie równobocznym, mamy

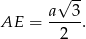
√ -- a--3- AE = 2 .

Wiemy ponadto, że środek trójkąta równobocznego dzieli jego wysokość w stosunku 2:1 (licząc od wierzchołka), czyli

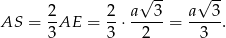
√ -- √ -- 2 2 a 3 a 3 AS = -AE = --⋅----- = -----. 3 3 2 3

Piszemy teraz twierdzenie Pitagorasa w trójkącie 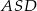ASD .

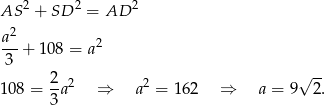
AS 2 + SD 2 = AD 2 a2- 2 3 + 108 = a 2 √ -- 108 = -a2 ⇒ a2 = 1 62 ⇒ a = 9 2 . 3

Zatem objętość czworościanu jest równa (ze wzoru na pole trójkąta równobocznego)

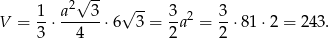
2√ -- √ -- V = 1⋅ a---3-⋅6 3 = 3a2 = 3-⋅8 1⋅2 = 243. 3 4 2 2

Teraz liczymy pole powierzchni całkowitej.

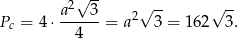
2√ -- √ -- √ -- Pc = 4 ⋅ a--3-= a2 3 = 162 3. 4

Odpowiedź: √ -- V = 243 , Pc = 1 62 3

Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!

Dodaj komentarz