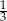Zadanie nr 9878711
We wnętrzu sześcianu umieszczono czworościan foremny w ten sposób, że wszystkie krawędzie czworościanu są przekątnymi ścian bocznych sześcianu. Wyznacz stosunek objętości czworościanu do objętości sześcianu.
Rozwiązanie
Szkicujemy opisaną sytuację.
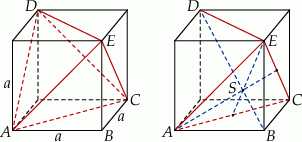
Oznaczmy przez  długość krawędzi sześcianu. Objętość sześcianu jest więc równa
długość krawędzi sześcianu. Objętość sześcianu jest więc równa 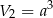 .
.
Sposób I
Zauważmy, że czworościan 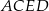 możemy otrzymać odcinając od sześcianu cztery ostrosłupy (naroża) takie jak
możemy otrzymać odcinając od sześcianu cztery ostrosłupy (naroża) takie jak 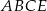 . Objętość jednego takiego ostrosłupa jest równa
. Objętość jednego takiego ostrosłupa jest równa
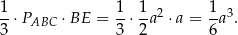
Objętość czworościanu 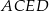 jest więc równa
jest więc równa
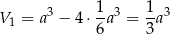
i interesujący nas stosunek objętości jest równy
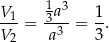
Sposób II
Tym razem będziemy mniej sprytni i bardziej wprost obliczymy objętość czworościanu 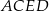 . Jego podstawą jest trójkąt równoboczny
. Jego podstawą jest trójkąt równoboczny 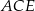 o boku długości
o boku długości 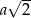 i polu
i polu
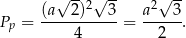
Wysokość  można obliczyć na różne sposoby – my patrzymy na trójkąt prostokątny
można obliczyć na różne sposoby – my patrzymy na trójkąt prostokątny  .
.
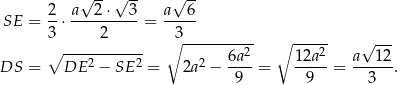
Objętość czworościanu 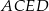 jest więc równa
jest więc równa
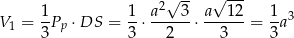
i interesujący nas stosunek objętości jest równy
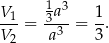
Odpowiedź: