Zadanie nr 2137854
Okno na poddaszu ma mieć kształt trapezu równoramiennego, którego przekątna ma długość 6 dm. Oblicz, jakie jest największe możliwe pole powierzchni tego okna.
Rozwiązanie
Szkicujemy trapez równoramienny.
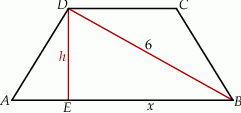
Sposób I
Zauważmy, że
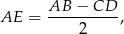
więc jeżeli oznaczymy 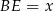 , to
, to
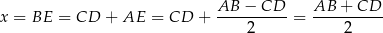
i pole trapezu jest równe
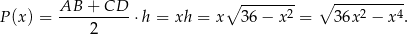
Musimy ustalić jaka jest największa możliwa wartość tej funkcji dla 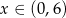 (bo
(bo 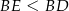 ). Funkcja
). Funkcja 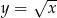 jest rosnąca, więc wystarczy zająć się funkcją
jest rosnąca, więc wystarczy zająć się funkcją
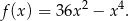
Liczymy pochodną
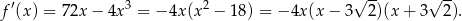
Widać teraz, że pochodna jest dodatnia w przedziale 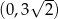 i ujemna w przedziale
i ujemna w przedziale 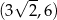 . To oznacza, że funkcja
. To oznacza, że funkcja 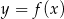 jest rosnąca w przedziale
jest rosnąca w przedziale 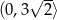 i malejąca w przedziale
i malejąca w przedziale 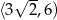 . To oznacza, że największą możliwą wartość pola trapezu otrzymamy dla
. To oznacza, że największą możliwą wartość pola trapezu otrzymamy dla 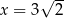 . Pole jest wtedy równe
. Pole jest wtedy równe
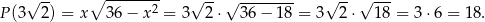
Sposób II
Jeżeli oznaczymy przez  miarę kąta między przekątnymi trapezu, to na mocy wzoru na pole czworokąta z przekątnymi, mamy
miarę kąta między przekątnymi trapezu, to na mocy wzoru na pole czworokąta z przekątnymi, mamy
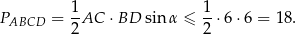
Równość zachodzi w tej nierówności, gdy 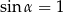 , czyli gdy przekątne trapezu są prostopadłe. Pole ma taką wartość np. dla kwadratu o boku
, czyli gdy przekątne trapezu są prostopadłe. Pole ma taką wartość np. dla kwadratu o boku 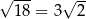 .
.
Odpowiedź: