Zadanie nr 3626376
W trójkąt prostokątny o przyprostokątnych długości 6 i 8 wpisujemy prostokąt w taki sposób, że dwa jego boki zawarte są w przyprostokątnych, a jeden z jego wierzchołków leży na przeciwprostokątnej. Zbadaj, jakie powinny być wymiary prostokąta, aby jego pole było możliwie największe.
Rozwiązanie
Zacznijmy od rysunku, przyjmijmy, że 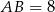 i
i 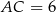 .
.
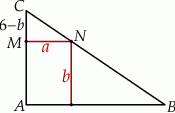
Z podobieństwa trójkątów 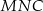 i
i 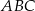 mamy
mamy
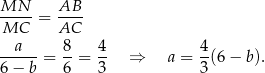
Musimy znaleźć taką wartość 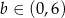 , dla której funkcja
, dla której funkcja
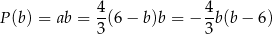
przyjmuje największą wartość. Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych w dół, osiąga ona największą wartość w wierzchołku, czyli dla 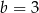 (środek odcinka łączącego miejsca zerowe). Wtedy
(środek odcinka łączącego miejsca zerowe). Wtedy 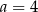 .
.
Odpowiedź: 3 cm x 4 cm

