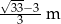Zadanie nr 3906205
Z odcinka drutu o długości 4 m wykonano ramkę w kształcie rombu z jedną przekątną (zobacz rysunek).
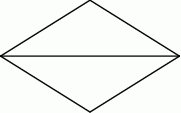
Jaka powinna być długość tej przekątnej, aby pole powierzchni tego rombu było największe możliwe?
Rozwiązanie
Oznaczmy przez  długość boku rombu.
długość boku rombu.
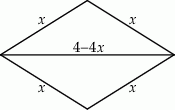
Przekątna ma wtedy długość
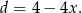
Sposób I
Pole rombu możemy obliczyć ze wzoru Herona
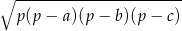
na pole trójkąta o bokach długości 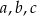 i obwodzie
i obwodzie 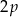 . W naszej sytuacji mamy
. W naszej sytuacji mamy
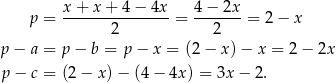
Pole rombu jest więc równe
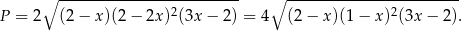
W tym miejscu zastanówmy się jeszcze jaka jest dziedzina tej funkcji. Muszą być spełnione warunki:
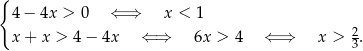
Dziedziną funkcji jest więc przedział 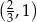 .
.
Pozostało ustalić jaka jest największa możliwa wartość funkcji
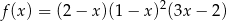
na przedziale 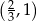 .
.
Jeżeli nie chcemy za dużo się naliczyć, to musimy wykazać się odrobiną sprytu. Zapiszmy wzór funkcji 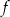 w postaci
w postaci
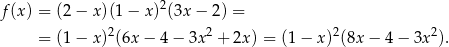
Liczymy teraz pochodną korzystając ze wzoru na pochodną iloczynu.
![′ [ 2]′ 2 2 2 ′ f (x) = (1 − x ) ⋅(8x − 4 − 3x ) + (1 − x) ⋅(8x − 4 − 3x ) = 2 2 = − 2(1 − x )(8x − 4− 3x )+ (1− x) (8− 6x) = = 2(1 − x )(3x2 − 8x + 4)+ 2(1 − x)(1 − x)(4 − 3x ) = = 2(1 − x )(3x2 − 8x + 4+ 4− 7x + 3x2) = 2(1− x)(6x2 − 15x + 8).](https://img.zadania.info/zad/3906205/HzadR14x.gif)
Rozkładamy jeszcze trójmian w nawiasie
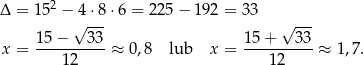
Pochodna jest więc równa
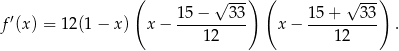
W interesującej nas dziedzinie funkcji pierwszy nawias jest zawsze dodatni, ostatni jest zawsze ujemny, więc pochodna jest dodatnia na przedziale 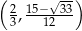 i ujemna na przedziale
i ujemna na przedziale 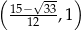 . W takim razie funkcja
. W takim razie funkcja 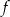 rośnie w przedziale
rośnie w przedziale 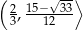 i maleje w przedziale
i maleje w przedziale 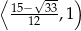 . Największe pole otrzymamy więc dla
. Największe pole otrzymamy więc dla 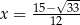 . Przekątna ma wtedy długość
. Przekątna ma wtedy długość
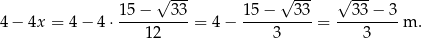
Sposób II
Tak jak poprzednio dochodzimy do problemu wyznaczenia największej wartości funkcji
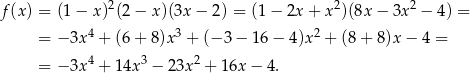
Liczymy pochodną
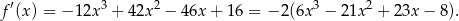
Szukamy teraz pierwiastków tego wielomianu – tak się szczęśliwie składa, że jednym z nich jest 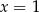 . Dzielimy teraz ten wielomian przez
. Dzielimy teraz ten wielomian przez 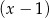 . My zrobimy to grupując wyrazy.
. My zrobimy to grupując wyrazy.
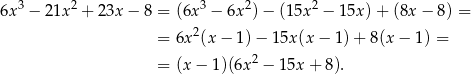
Rozkładamy jeszcze trójmian w nawiasie
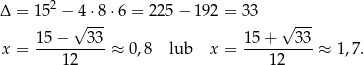
Pochodna jest więc równa
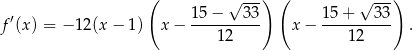
Dalszą część rozwiązania prowadzimy tak samo jak w sposobie I.
Sposób III
Pole rombu możemy oczywiście obliczyć bez użycia wzoru Herona. Z twierdzenia Pitagorasa obliczamy długość drugiej przekątnej rombu
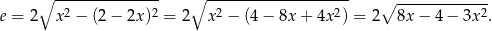
Pole rombu jest więc równe
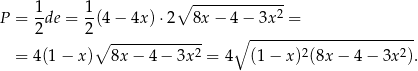
Dalszą część rozwiązania przeprowadzamy tak samo jak w jednym z poprzednich sposobów.
Odpowiedź: