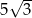/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Największe pole

Zadanie nr 4388232

W trójkąt prostokątny o kącie ostrym 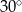∘ 30 i przeciwprostokątnej długości 40 cm wpisujemy prostokąty w ten sposób, że jeden bok każdego z tych prostokątów zawiera się w przeciwprostokątnej trójkąta. Zbadaj który z tych prostokątów ma największe pole.

Wersja PDF

Rozwiązanie

Zacznijmy od rysunku i oznaczmy boki prostokąta przez a i b .

PIC

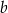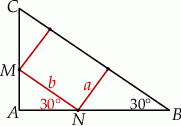
Z definicji funkcji trygonometrycznych w odpowiednich trójkątach mamy

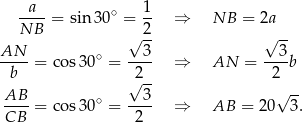
-a--= sin 30∘ = 1- ⇒ NB = 2a NB 2- -- AN √ 3 √ 3 ---- = co s30∘ = ---- ⇒ AN = ---b b √2-- 2 AB-- ∘ --3- √ -- CB = co s30 = 2 ⇒ AB = 20 3.

Zatem

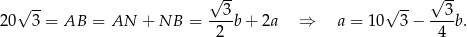
√ -- √ -- √ -- 3 √ -- 3 20 3 = AB = AN + NB = --2-b+ 2a ⇒ a = 1 0 3− -4-b .

Pozostało wyznaczyć taką wartość 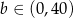b ∈ (0,40) , dla której funkcja

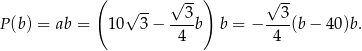
( -- √ --) √ -- P(b ) = ab = 10√ 3 − ---3b b = − --3(b − 40)b. 4 4

osiąga największą wartość. Ponieważ wykresem tej funkcji jest parabola o ramionach skierowanych w dół i miejscach zerowych 0 i 40, funkcja ta przyjmuje największą wartość w wierzchołku, czyli dla 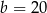b = 2 0 . Wtedy √ -- a = 5 3 .  
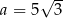Odpowiedź: Bok na przeciwprostokątnej: 20, drugi bok: √ -- 5 3

Wersja PDF