Zadanie nr 4822301
Arkusz blachy ma kształt trójkąta prostokątnego 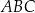 , w którym
, w którym 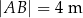 i
i 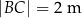 . Z tego arkusza należy wyciąć trójkąt równoramienny
. Z tego arkusza należy wyciąć trójkąt równoramienny 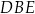 w ten sposób, że punkty
w ten sposób, że punkty 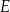 i
i 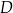 leżą odpowiednio na odcinkach
leżą odpowiednio na odcinkach 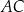 i
i 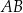 oraz
oraz 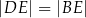 (zobacz rysunek).
(zobacz rysunek).
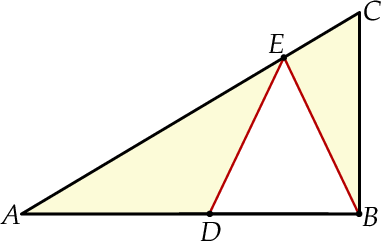
Oblicz jaką długość powinna mieć podstawa 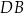 trójkąta
trójkąta 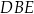 tak, aby jego pole było największe możliwe. Oblicz to największe pole.
tak, aby jego pole było największe możliwe. Oblicz to największe pole.
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.

