Zadanie nr 5131914
Obwód trapezu równoramiennego kącie ostrym 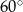 równa się
równa się 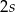 (
(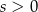 ). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
). Jakie powinny być wymiary tego trapezu, aby jego pole było największe? Oblicz to największe pole.
Rozwiązanie
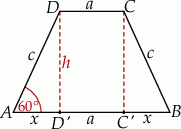
Jak zwykle zaczynamy od rysunku. Oznaczmy  – długość krótszej podstawy,
– długość krótszej podstawy,  – długość ramienia,
– długość ramienia, 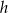 – długość wysokości,
– długość wysokości,  – długość odcinka
– długość odcinka 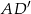 .
.
Korzystamy z trójkąta prostokątnego 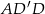 i obliczymy:
i obliczymy: 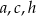 . Potem obliczamy też pole, w zależności od
. Potem obliczamy też pole, w zależności od  .
.
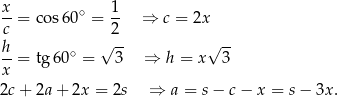
Możemy teraz obliczyć pole
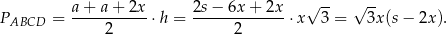
Wykres otrzymanej funkcji to parabola o ramionach skierowanych w dół. Jej wierzchołek znajduje się dokładnie w połowie między miejscami zerowymi, czyli w połowie odcinka 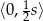 . Największa wartość pola otrzymamy zatem dla
. Największa wartość pola otrzymamy zatem dla 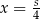 . Z poprzednich obliczeń mamy wtedy
. Z poprzednich obliczeń mamy wtedy 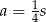 ,
, 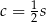 , a dłuższa podstawa to
, a dłuższa podstawa to 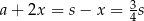 . Pole trapezu jest wtedy równe
. Pole trapezu jest wtedy równe
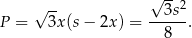
Odpowiedź: Podstawy: 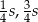 , ramiona:
, ramiona: 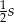 , pole:
, pole: 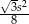 .
.

