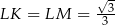Zadanie nr 6138320
W kwadracie  o boku długości 1 na boku
o boku długości 1 na boku  wybrano punkt
wybrano punkt  . Na bokach
. Na bokach 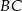 i
i 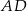 wybrano odpowiednio punkty
wybrano odpowiednio punkty 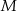 i
i 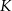 tak, że
tak, że 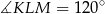 , a dwusieczna tego kąta jest równoległa do boku
, a dwusieczna tego kąta jest równoległa do boku 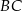 . Oblicz długości odcinków
. Oblicz długości odcinków 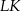 i
i 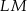 , dla których pole trójkąta
, dla których pole trójkąta 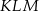 jest największe.
jest największe.
Rozwiązanie
Rozpoczynamy od rysunku.
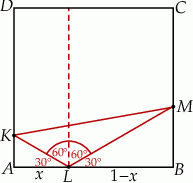
Oznaczmy 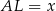 , wtedy
, wtedy 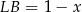 .
.
Sposób I
Z trójkątów prostokątnych 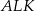 i
i 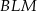 obliczamy długości boków
obliczamy długości boków 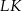 i
i 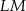 trójkąta
trójkąta  .
.
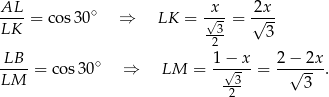
Pole trójkąta  jest więc równe (korzystamy ze wzoru z sinusem).
jest więc równe (korzystamy ze wzoru z sinusem).
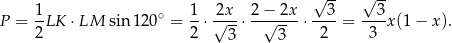
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół i miejscach zerowych 0 i 1. Największą wartość pola otrzymamy więc w wierzchołku tej paraboli, czyli dokładnie w środku między pierwiastkami: 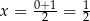 . Odcinki
. Odcinki 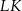 i
i 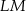 mają wtedy długości.
mają wtedy długości.
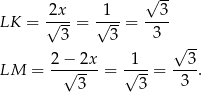
Sposób II
Zamiast sprawdzać, kiedy pole trójkąta 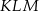 jest największe, sprawdźmy kiedy pole pozostałej części kwadratu jest najmniejsze. Z trójkątów prostokątnych
jest największe, sprawdźmy kiedy pole pozostałej części kwadratu jest najmniejsze. Z trójkątów prostokątnych 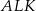 i
i 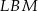 mamy
mamy
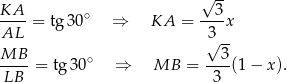
Obliczamy teraz sumę pól trójkątów prostokątnych 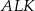 i
i 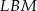 oraz trapezu prostokątnego
oraz trapezu prostokątnego 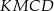 .
.
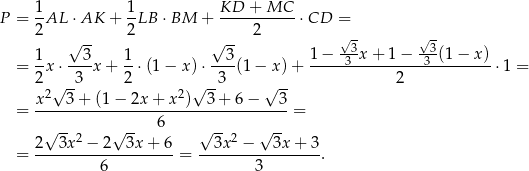
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, więc najmniejszą wartość pola otrzymamy w wierzchołku tej paraboli, czyli dla
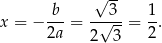
Mamy wtedy
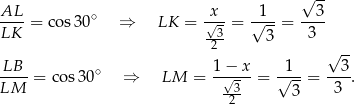
Odpowiedź: