Zadanie nr 6820951
W trójkąt prostokątny 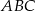 , w którym
, w którym 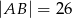 ,
, 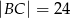 ,
, 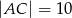 , wpisujemy prostokąty
, wpisujemy prostokąty 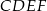 , tak, że punkt
, tak, że punkt 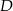 należy do boku
należy do boku 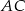 , pkt
, pkt 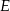 należy do boku
należy do boku 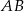 i punkt
i punkt 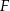 należy do boku
należy do boku 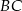 . Oblicz wymiary prostokąta o największym polu.
. Oblicz wymiary prostokąta o największym polu.
Rozwiązanie
Zaczynamy od rysunku.
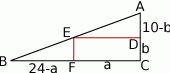
Z podobieństwa trójkątów 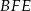 i
i 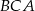 mamy
mamy
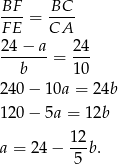
Zatem pole prostokąta jest równe
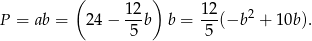
Jest to więc parabola o ramionach skierowanych w dół. Największą wartość pola otrzymamy więc w wierzchołku praboli, czyli dla 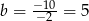 . Wtedy
. Wtedy 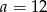 .
.
Odpowiedź: Boki prostokąta: 5 i 12

