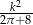/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Największe pole

Zadanie nr 6853927

Przedstawiona na rysunku figura składa się z półkola i prostokąta. Oblicz maksymalne pole tej figury, jeżeli jej obwód jest równy 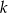k .

PIC

Wersja PDF

Rozwiązanie

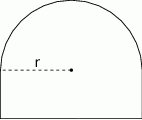
Jeżeli (tak jak na obrazku) oznaczymy promień półkola przez r , a pionowy bok prostokąta przez a , to z podanego obwodu mamy

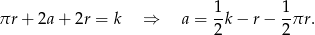
πr + 2a+ 2r = k ⇒ a = 1k − r− 1πr . 2 2

Pole figury jest więc równe

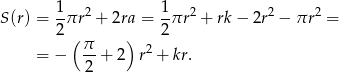
1 1 S(r) = --πr2 + 2ra = -πr 2 + rk − 2r2 − πr 2 = 2 ( ) 2 = − π-+ 2 r2 + kr. 2

wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największe pole otrzymamy w wierzchołku, czyli dla

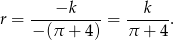
r = ----−k---- = ---k--. − (π + 4) π + 4

Największe pole jest więc równe

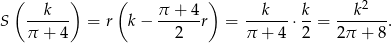
( ) ( ) 2 --k--- π-+-4- --k--- k- ---k--- S π + 4 = r k− 2 r = π + 4 ⋅2 = 2π + 8.

 
Odpowiedź: --k2- 2π+ 8

Wersja PDF