Zadanie nr 7180228
Długości boków prostokąta 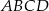 spełniają warunki:
spełniają warunki: 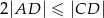 i
i 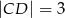 . Na boku
. Na boku 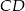 wybrano punkty
wybrano punkty 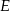 i
i 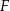 w ten sposób, że
w ten sposób, że 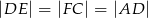 . Punkt
. Punkt 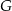 jest takim punktem odcinka
jest takim punktem odcinka 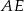 , że
, że 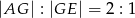 . Oblicz długość boku
. Oblicz długość boku 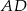 prostokąta, dla której pole trójkąta
prostokąta, dla której pole trójkąta 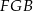 jest największe.
jest największe.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
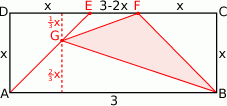
Pole trójkąta 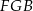 obliczymy odejmując od pola prostokąta pola 4 białych trójkątów (inny sposób to od pola trapezu
obliczymy odejmując od pola prostokąta pola 4 białych trójkątów (inny sposób to od pola trapezu 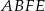 odjąć pola trójkątów
odjąć pola trójkątów 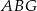 i
i 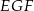 ).
).
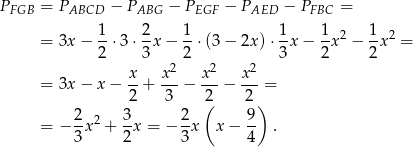
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość przyjmuje dokładnie w środku między pierwiastkami, czyli dla 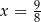 .
.
Odpowiedź: