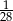Zadanie nr 7228546
Dany jest romb 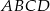 o boku długości 1, w którym kąt
o boku długości 1, w którym kąt 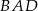 jest ostry i
jest ostry i 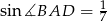 . Na bokach
. Na bokach 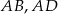 i
i 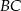 wybrano odpowiednio punkty
wybrano odpowiednio punkty 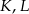 i
i 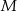 w ten sposób, że odcinki
w ten sposób, że odcinki 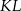 i
i 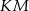 są równoległe do przekątnych rombu.
są równoległe do przekątnych rombu.
- Oblicz pole czworokąta
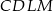 .
. - Oblicz największą możliwą wartość pola trójkąta
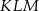 .
.
Rozwiązanie
- Rozpoczynamy oczywiście od rysunku.
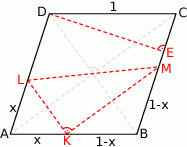
Zauważmy, że czworokąt
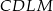 jest trapezem, którego wysokość jest równa wysokości rombu. Obliczmy więc najpierw wysokość rombu. Z trójkąta prostokątnego
jest trapezem, którego wysokość jest równa wysokości rombu. Obliczmy więc najpierw wysokość rombu. Z trójkąta prostokątnego 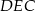 mamy
mamy 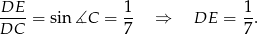
Zauważmy, że trójkąty
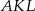 i
i 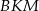 są podobne odpowiednio do
są podobne odpowiednio do 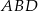 i
i 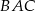 , czyli są równoramienne. Oznaczmy
, czyli są równoramienne. Oznaczmy 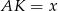 . Wtedy
. Wtedy 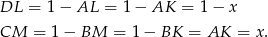
Teraz bez problemu obliczamy pole trapezu
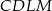
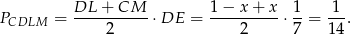
Odpowiedź: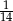
-
Sposób I
Z poprzedniego podpunktu wiemy, że pole czworokąta
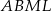 stanowi połowę pola rombu (bo pole rombu jest równe
stanowi połowę pola rombu (bo pole rombu jest równe  ). W szczególności pole tego czworokąta jest stałe i nie zależy od wyboru punktu
). W szczególności pole tego czworokąta jest stałe i nie zależy od wyboru punktu 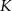 . To oznacza, że pole trójkąta
. To oznacza, że pole trójkąta 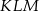 będzie największe, gdy suma pól trójkątów
będzie największe, gdy suma pól trójkątów 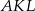 i
i 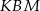 będzie najmniejsza. Obliczmy tę sumę (jak w poprzednim podpunkcie przyjmujemy
będzie najmniejsza. Obliczmy tę sumę (jak w poprzednim podpunkcie przyjmujemy 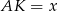 ).
). 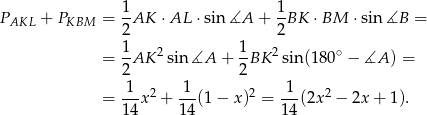
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w górę, która najmniejszą wartość przyjmuje w wierzchołku, czyli dla
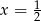 . Mamy wtedy
. Mamy wtedy 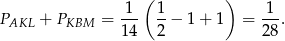
Zatem
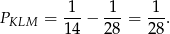
Sposób II
Tym razem, korzystając z twierdzenia cosinusów, obliczymy wprost pole trójkąta
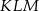 . Obliczmy najpierw
. Obliczmy najpierw 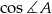 i
i 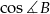 .
. 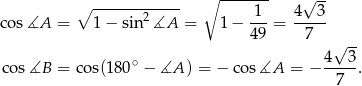
Liczymy długości odcinków
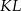 i
i  .
. 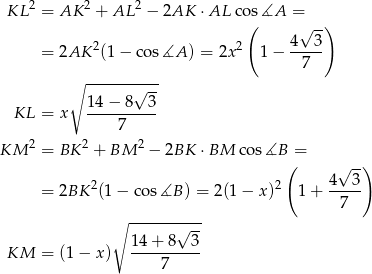
Trójkąt
 jest prostokątnym, więc
jest prostokątnym, więc 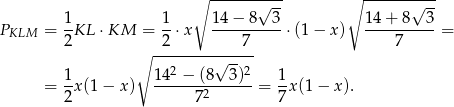
wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość otrzymamy w wierzchołku, czyli dla
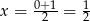 (w środku między pierwiastkami). Wartość funkcji jest wtedy równa
(w środku między pierwiastkami). Wartość funkcji jest wtedy równa 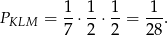
Odpowiedź: