Zadanie nr 7627989
Rozpatrujemy wszystkie czworokąty 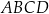 , które są jednoczenie wpisane w okrąg i opisane na okręgu, w których
, które są jednoczenie wpisane w okrąg i opisane na okręgu, w których 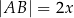 ,
, 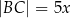 , i których obwód jest równy 10.
, i których obwód jest równy 10.
Pole czworokąta 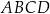 wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
wpisanego w okrąg można obliczyć ze wzoru Brahmagupty
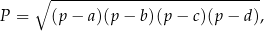
gdzie 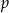 – jest połową obwodu czworokąta.
– jest połową obwodu czworokąta.
Zapisz pole czworokąta 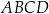 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.
. Wyznacz dziedzinę tej funkcji i oblicz długości boków tego z rozważanych czworokątów, którego pole jest największe.
Rozwiązanie
Szkicujemy czworokąt 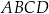 .
.

Ponieważ czworokąt jest opisany na okręgu, sumy długości jego przeciwległych boków są równe. Sumy te muszą być równe połowie obwodu 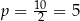 i mamy
i mamy
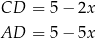
Pole czworokąta jest więc równe
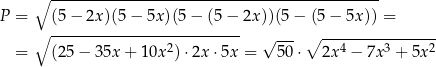
Aby wyznaczyć dziedzinę zauważmy, że oczywiście 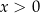 , oraz
, oraz 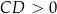 i
i 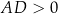 . Dziedziną tej funkcji jest więc przedział
. Dziedziną tej funkcji jest więc przedział 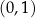 .
.
Liczymy teraz pochodną funkcji
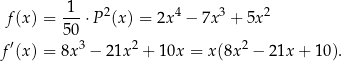
Rozkładamy trójmian w nawiasie.
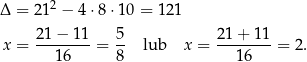
Mamy zatem
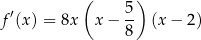
To oznacza, że w przedziale 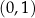 pochodna: jest dodatnia dla
pochodna: jest dodatnia dla 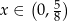 i ujemna dla
i ujemna dla 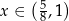 . To oznacza, że funkcja
. To oznacza, że funkcja 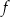 rośnie w przedziale
rośnie w przedziale 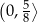 i maleje w przedziale
i maleje w przedziale 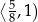 . W takim razie największą wartość pola otrzymamy dla
. W takim razie największą wartość pola otrzymamy dla 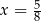 . Długości boków czworokąta są wtedy równe
. Długości boków czworokąta są wtedy równe
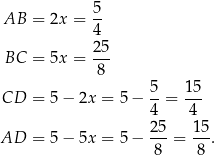
Odpowiedź: 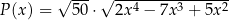 dla
dla 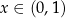 , boki:
, boki: 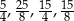 .
.

