Zadanie nr 8998621
Rozpatrujemy trapezy równoramienne 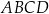 o przekątnej długości 1 i sumie długości podstaw równej
o przekątnej długości 1 i sumie długości podstaw równej  . Zapisz pole trapezu
. Zapisz pole trapezu 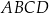 jako funkcję zmiennej
jako funkcję zmiennej  . Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
. Wyznacz dziedzinę tej funkcji i oblicz sumę długości podstaw tego z rozważanych trapezów, którego pole jest największe. Oblicz to największe pole.
Rozwiązanie
Szkicujemy trapez równoramienny.
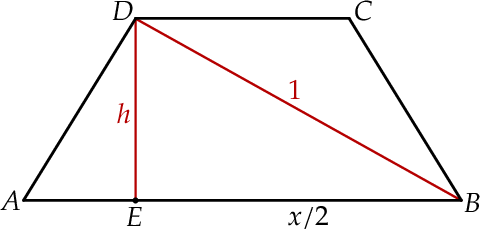
Zauważmy, że
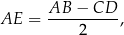
więc
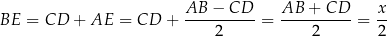
i pole trapezu jest równe
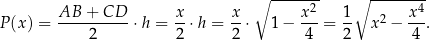
Aby wyznaczyć dziedzinę tej funkcji zauważmy, że oczywiście 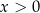 oraz
oraz 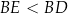 , czyli
, czyli 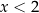 . Dziedziną jest więc przedział
. Dziedziną jest więc przedział 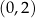 .
.
Musimy teraz ustalić jaka jest największa możliwa wartość tej funkcji. Funkcja 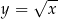 jest rosnąca, więc wystarczy zająć się funkcją
jest rosnąca, więc wystarczy zająć się funkcją
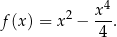
Liczymy pochodną
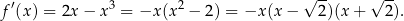
Widać teraz, że pochodna jest dodatnia w przedziale 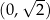 i ujemna w przedziale
i ujemna w przedziale 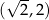 . To oznacza, że funkcja
. To oznacza, że funkcja 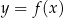 jest rosnąca w przedziale
jest rosnąca w przedziale 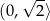 i malejąca w przedziale
i malejąca w przedziale 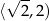 . Zatem największą możliwą wartość pola trapezu otrzymamy dla
. Zatem największą możliwą wartość pola trapezu otrzymamy dla 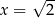 . Pole jest wtedy równe
. Pole jest wtedy równe
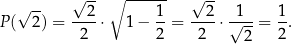
Odpowiedź: 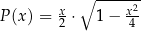 dla
dla 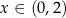 ,
, 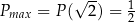 .
.

