/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Największe pole

Zadanie nr 9024223

Dodaj do ulubionych
Dodaj do rozwiązanych

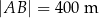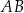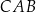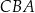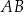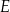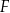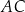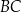Działka ma kształt trójkąta o podstawie |AB | = 400 m . Wysokość trójkąta opuszczona na podstawę AB jest równa 125 m, a jego kąty CAB i CBA są ostre. Z działki postanowiono wydzielić plac w kształcie prostokąta z przeznaczeniem na parking. Dwa z wierzchołków tego prostokąta mają leżeć na podstawie AB tego trójkąta, a dwa pozostałe – E oraz F – na bokach AC i BC trójkąta (zobacz rysunek).

ZINFO-FIGURE

Wyznacz długości boków prostokąta, dla których powierzchnia wydzielonego placu będzie największa. Wyznacz tę największą powierzchnię.

Rozwiązanie

Oznaczmy przez a długość boku parkingu zwartego w podstawie AB , a przez b długość boku prostopadłego do podstawy AB .

Sposób I

Mamy wtedy

PABC = PABED + PDEC 1- 400-+-a- 1- 2 ⋅40 0⋅12 5 = 2 ⋅b + 2 ⋅a ⋅(125 − b) / ⋅2 5000 0 = 400b + ab + 12 5a− ab / : 1 25 a = 400 − 3,2b.

Musimy więc wyznaczyć największą wartość funkcji

f (b) = ab = (400 − 3 ,2b )b = 3,2(12 5− b )b

określonej dla b ∈ (0,125) . Wykresem tej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość otrzymamy w wierzchołku, czyli dla b = 125+2-0= 62,5 . Pole powierzchni parkingu jest wtedy równe

f (62,5) = 3,2 ⋅62,5 ⋅62,5 = 12500 m 2.

Drugi bok parkingu ma długość

a = 400− 3,2b = 40 0− 200 = 200 m .

Sposób II

Trójkąty CDE i CAB są podobne w skali

k = 1-25−--b 1 25

(z prawej strony mamy iloraz wysokości tych trójkątów). Mamy zatem

125-−-b- DE-- --a- 125 = k = AB = 4 00 / ⋅4 00 3,2(12 5− b) = a.

Dalszą część rozwiązania przeprowadzamy tak samo jak w poprzednim sposobie.  
Odpowiedź: 62,5 m × 200 m , P = 12500 m 2

Wersja PDF