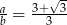/Szkoła średnia/Geometria/Planimetria/Zadania na ekstrema/Największe pole

Zadanie nr 9096994

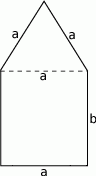
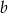Obwód okna przedstawionego na rysunku wynosi 7 m. W jakim stosunku powinny pozostawać odcinki a i b , aby przez okno wpadało jak najwięcej światła?

PIC

Wersja PDF

Rozwiązanie

Liczymy pole okna (bo od niego zależy ilość wpadającego światła). Pole jest sumą pola trójkąta równobocznego i prostokąta, więc jest równe

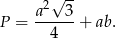
2√ -- P = a---3-+ ab. 4

Wykorzystajmy jeszcze informację o obwodzie.

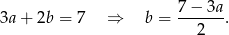
3a + 2b = 7 ⇒ b = 7−--3a. 2

Zatem pole jest równe

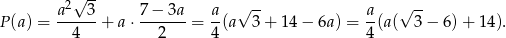
2√ -- √ -- √ -- P (a) = a---3-+ a⋅ 7-−-3a = a-(a 3+ 14− 6a) = a-(a( 3 − 6)+ 14). 4 2 4 4

Wykresem tej funkcji jest parabola o ramionach skierowanych w dół (bo 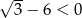√ -- 3 − 6 < 0 !), zatem największą wartość pola otrzymamy w wierzchołku, czyli dla

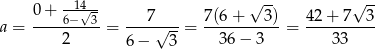
-14-- √ -- √ -- 0+--6−√-3- ---7---- 7(6-+---3)- 42-+-7--3- a = 2 = 6 − √ 3-= 36 − 3 = 33

(dokładnie pomiędzy pierwiastkami). Zatem szukany stosunek wynosi

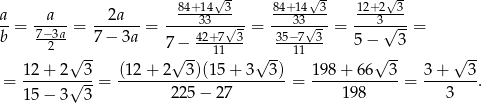
√ - √ - √- a a 2a 84+3134-3- 84+3143--3 12+23-3- --= 7−3a-= -------= ----42+7√3-= -35−7√3- = ---√----= b 2 7 − 3a 7− --11--- --11--- 5− 3 √ -- √ -- √ -- √ -- √ -- = 12-+-2-√-3-= (12-+-2---3)(15+--3--3) = 198-+-66--3-= 3-+---3. 15 − 3 3 2 25− 27 198 3

 
Odpowiedź: a 3+√-3 b = 3

Wersja PDF