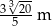Zadanie nr 5078090
Firma logistyczna planuje produkcję pojemników w kształcie graniastosłupa prostego o objętości 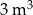 i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za
i podstawie będącej prostokątem, w którym jeden z boków jest 4 razy dłuższy od drugiego. Koszt materiału potrzebnego do produkcji ścian bocznych tego pojemnika wynosi 40 zł za 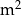 , a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za
, a koszt materiału potrzebnego do produkcji jego górnej i dolnej podstawy wynosi 60 zł za 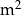 . Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
. Oblicz jakie powinny być wymiary tego pojemnika, aby koszt jego produkcji był najmniejszy możliwy.
Rozwiązanie
Szkicujemy graniastosłup.
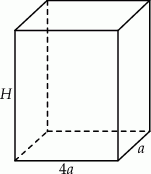
Zapiszmy podaną informację o objętości graniastosłupa.
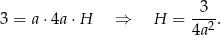
Koszt produkcji takiego pojemnika jest więc równy
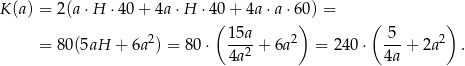
Wystarczy więc znaleźć wartość najmniejszą funkcji
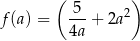
określonej dla 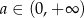 . Liczymy pochodną
. Liczymy pochodną
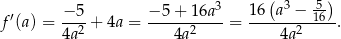
Widać teraz, że pochodna ma jedno miejsce zerowe
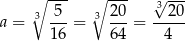
i pochodna zmienia znak z ujemnego na dodatni w tym punkcie. To oznacza, że funkcja 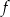 maleje w przedziale
maleje w przedziale 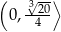 i rośnie w przedziale
i rośnie w przedziale 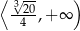 . Najmniejszy koszt produkcji pojemnika otrzymamy więc dla
. Najmniejszy koszt produkcji pojemnika otrzymamy więc dla 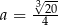 . Pozostałe krawędzie prostopadłościanu mają wtedy długości
. Pozostałe krawędzie prostopadłościanu mają wtedy długości
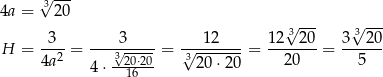
Odpowiedź: Podstawa: 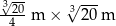 , wysokość:
, wysokość: