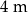Zadanie nr 5771596
Pewien zakład otrzymał zamówienie na wykonanie prostopadłościennego zbiornika (całkowicie otwartego od góry) o pojemności 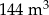 . Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
. Dno zbiornika ma być kwadratem. Żaden z wymiarów zbiornika (krawędzi prostopadłościanu) nie może przekraczać 9 metrów. Całkowity koszt wykonania zbiornika ustalono w następujący sposób:
– 100 zł za 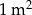 dna
dna
– 75 zł za 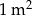 ściany bocznej.
ściany bocznej.
Oblicz wymiary zbiornika, dla którego tak ustalony koszt wykonania będzie najmniejszy.
Rozwiązanie
Szkicujemy graniastosłup.
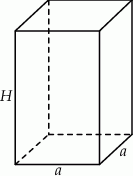
Zapiszmy podaną informację o objętości graniastosłupa.
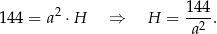
Koszt wykonania takiego zbiornika jest więc równy
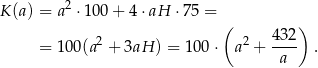
Wystarczy więc znaleźć wartość najmniejszą funkcji
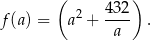
Aby ustalić jaka jest dziedzina tej funkcji musimy wykorzystać podaną informację o maksymalnej długości krawędzi prostopadłościanu. Mamy zatem 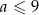 i
i
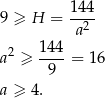
Dziedziną funkcji 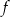 jest więc przedział
jest więc przedział 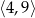 . Liczymy pochodną
. Liczymy pochodną
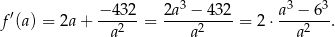
Widać teraz, że pochodna ma jedno miejsce zerowe 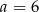 i pochodna zmienia znak z ujemnego na dodatni w tym punkcie. To oznacza, że funkcja
i pochodna zmienia znak z ujemnego na dodatni w tym punkcie. To oznacza, że funkcja  maleje w przedziale
maleje w przedziale  i rośnie w przedziale
i rośnie w przedziale 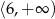 . Najmniejszy koszt wykonania pojemnika otrzymamy więc dla
. Najmniejszy koszt wykonania pojemnika otrzymamy więc dla 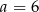 . Wysokość pojemnika jest wtedy równa
. Wysokość pojemnika jest wtedy równa
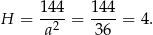
Odpowiedź: Krawędź podstawy: 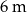 , wysokość:
, wysokość: