/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Najmniejsze pole

Zadanie nr 7200162

Dodaj do ulubionych
Dodaj do rozwiązanych

Zakład produkcyjny dostał zlecenie produkcji prostopadłościennych pudełek (całkowicie otwartych od góry) o objętości 60,75 litra. Dno pudełka ma być kwadratem i żaden z jego wymiarów nie może przekraczać 67,5 cm. Na koszt wykonania pudełka składają się – koszt wykonania 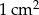1 cm 2 dna w wysokości 48 gorszy oraz koszt wykonania 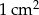2 1 cm ściany bocznej w wysokości 36 groszy. Oblicz wymiary pudełka, dla których koszt jego produkcji będzie najmniejszy.

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.