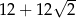Zadanie nr 1599032
Rozpatrujemy wszystkie ostrosłupy prawidłowe czworokątne o krawędzi bocznej równej 3. Oblicz pole powierzchni całkowitej tego z tych ostrosłupów, dla którego pole przekroju płaszczyzną przechodzącą przez środki dwóch sąsiednich krawędzi podstawy oraz wierzchołek ostrosłupa jest największe możliwe.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
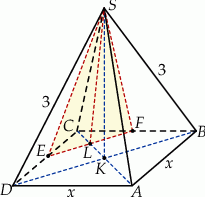
Niech 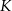 będzie środkiem kwadratu w podstawie ostrosłupa oraz
będzie środkiem kwadratu w podstawie ostrosłupa oraz 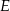 i
i 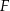 niech będą środkami krawędzi
niech będą środkami krawędzi 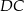 i
i 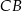 . Oznaczmy też przez
. Oznaczmy też przez  długość krawędzi podstawy ostrosłupa. Przekrój
długość krawędzi podstawy ostrosłupa. Przekrój 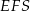 jest trójkątem równoramiennym o podstawie
jest trójkątem równoramiennym o podstawie
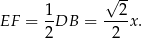
Jego wysokość 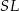 możemy obliczyć z trójkąta prostokątnego
możemy obliczyć z trójkąta prostokątnego 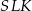 .
.
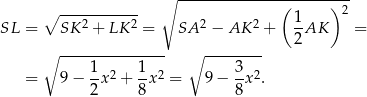
Pole trójkąta 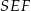 jest więc równe
jest więc równe
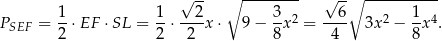
Badamy teraz przebieg zmienności funkcji
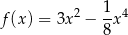
określonej dla 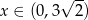 (bo musi być spełniony warunek
(bo musi być spełniony warunek 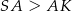 ). Liczymy pochodną
). Liczymy pochodną
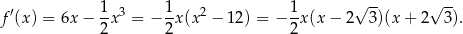
Widać teraz, że pochodna jest dodatnia dla 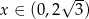 i ujemna dla
i ujemna dla 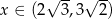 . To oznacza, że funkcja
. To oznacza, że funkcja 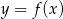 rośnie w przedziale
rośnie w przedziale 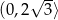 i maleje w przedziale
i maleje w przedziale 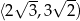 . W takim razie pole trójkąta
. W takim razie pole trójkąta 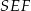 jest największe jeżeli
jest największe jeżeli 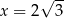 . Pozostało obliczyć pole powierzchni bocznej ostrosłupa.
. Pozostało obliczyć pole powierzchni bocznej ostrosłupa.
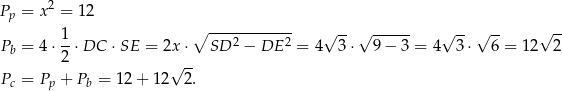
Odpowiedź: