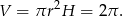Zadanie nr 4035127
W trójkąt prostokątny o przyprostokątnych o długościach 2 i 4 wpisano prostokąt w ten sposób, że dwa jego boki leżą na przyprostokątnych trójkąta, a jeden z wierzchołków prostokąta leży na przeciwprostokątnej trójkąta. Prostokąt ten obraca się dookoła prostej, zawierającej dłuższą przyprostokątną trójkąta, tworząc walec. Oblicz, który z walców, otrzymanych w powyższy sposób, posiada największe pole powierzchni bocznej i oblicz jego objętość.
Rozwiązanie
Zaczynijmy od rysunku i oznaczmy promień podstawy walca przez  , a jego wysokość przez
, a jego wysokość przez 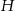 .
.
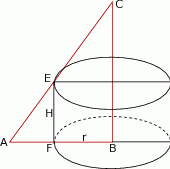
Z podobieństwa trójkąctów 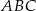 i
i 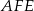 mamy
mamy
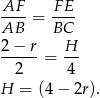
Liczymy pole powierzchni bocznej
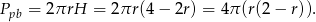
Wykres funkcji 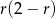 to parabola o ramionach skierowanych w dół. Zatem największe pole powierzchni bocznej otrzymamy w wierzchołku, czyli dla
to parabola o ramionach skierowanych w dół. Zatem największe pole powierzchni bocznej otrzymamy w wierzchołku, czyli dla 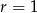 (środek odcinka łączącego pierwiastki). Wtedy
(środek odcinka łączącego pierwiastki). Wtedy 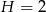 i objętość jest równa
i objętość jest równa