Zadanie nr 4358338
W ostrosłup prawidłowy czworokątny wpisujemy graniastosłupy prawidłowe czworokątne w ten sposób, że dolna podstawa graniastosłupa zawiera się podstawie ostrosłupa, a każdy z wierzchołków górnej podstawy należy do jednej z krawędzi bocznych ostrosłupa. Wiedząc, że każda z krawędzi ostrosłupa ma długość 6, oblicz jaka jest maksymalna możliwa powierzchnia boczna graniastosłupa.
Rozwiązanie
Rozpoczynamy oczywiście od dużego rysunku.
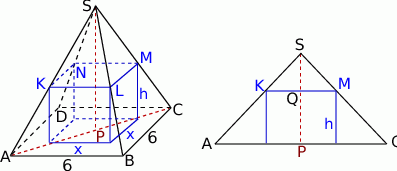
Gdy chwilkę poprzyglądamy się rysunkowi, powinno stać się jasne, że wszystko co jest godne uwagi w opisanej sytuacji rozgrywa się w trójkącie 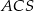 . Jest to trójkąt równoramienny o ramionach długości 6 i podstawie długości
. Jest to trójkąt równoramienny o ramionach długości 6 i podstawie długości 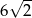 . Jego wysokość
. Jego wysokość 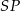 ma długość
ma długość
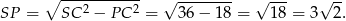
Oznaczmy przez 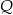 punkt wspólny wysokości
punkt wspólny wysokości 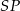 ostrosłupa oraz górnej podstawy graniastosłupa, przez
ostrosłupa oraz górnej podstawy graniastosłupa, przez 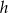 wysokość, a przez
wysokość, a przez  długość krawędzi podstawy graniastosłupa. W takim razie
długość krawędzi podstawy graniastosłupa. W takim razie 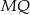 to połowa przekątnej w kwadracie o boku
to połowa przekątnej w kwadracie o boku  , czyli
, czyli
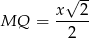
Z podobieństwa trójkątów 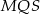 i
i 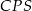 mamy
mamy
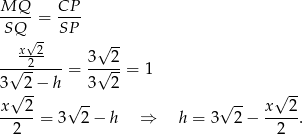
W takim razie pole powierzchni bocznej graniastosłupa jest równe
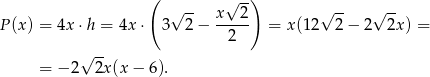
Wykresem otrzymanej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość pola otrzymamy w wierzchołku, czyli dla 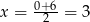 (dokładnie w środku między pierwiastkami). Pole powierzchni bocznej jest wtedy równe
(dokładnie w środku między pierwiastkami). Pole powierzchni bocznej jest wtedy równe
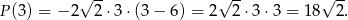
Odpowiedź: