/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Największe pole

Zadanie nr 5315224

Suma krawędzi graniastosłupa prawidłowego trójkątnego jest równa 3. Dla jakiej długości krawędzi podstawy pole powierzchni całkowitej tego graniastosłupa będzie największe?

Wersja PDF

Rozwiązanie

Szkicujemy graniastosłup trójkątny.

PIC

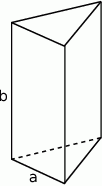
Oznaczmy długość krawędzi podstawy przez a , a długość krawędzi bocznej przez 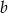b . Pole powierzchni całkowitej jest więc równe

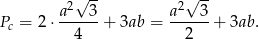
√ -- √ -- a-2--3 a2--3- Pc = 2 ⋅ 4 + 3ab = 2 + 3ab.

Wiemy ponadto, że

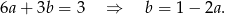
6a+ 3b = 3 ⇒ b = 1− 2a.

Podstawiamy to wyrażenie do wzoru na pole całkowite.

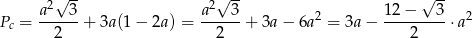
√ -- √ -- √ -- a2--3- a2--3- 2 12-−---3- 2 Pc = 2 + 3a (1− 2a) = 2 + 3a− 6a = 3a − 2 ⋅a

Wykresem powyższej funkcji jest parabola o ramionach skierowanych w dół, więc największą wartość pola otrzymamy w wierzchołku tej paraboli, czyli dla

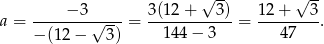
√ -- √ -- -----−-3----- 3(12-+---3)- 12-+---3- a = − (12 − √ 3) = 144 − 3 = 47 .

 
Odpowiedź: 12+-√3 47

Wersja PDF