Zadanie nr 7900319
Spodek wysokości ostrosłupa 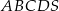 pokrywa się ze środkiem rombu
pokrywa się ze środkiem rombu 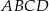 w jego podstawie oraz
w jego podstawie oraz 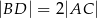 ,
, 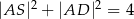 . Oblicz objętość ostrosłupa
. Oblicz objętość ostrosłupa 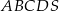 jeżeli wiadomo, że pole trójkąta
jeżeli wiadomo, że pole trójkąta 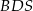 jest największe możliwe.
jest największe możliwe.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
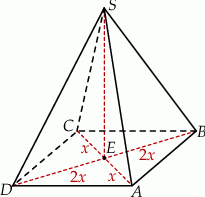
Niech 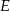 będzie środkiem rombu w podstawie i oznaczmy
będzie środkiem rombu w podstawie i oznaczmy 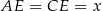 ,
, 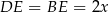 . Przekątne rombu są prostopadłe, więc
. Przekątne rombu są prostopadłe, więc
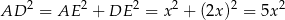
i
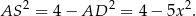
Stąd
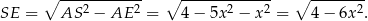
Pole trójkąta 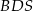 jest więc równe
jest więc równe
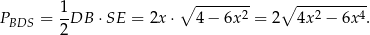
Badamy teraz przebieg zmienności funkcji
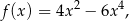
której dziedziną jest 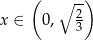 (bo
(bo 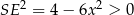 ). Liczymy pochodną
). Liczymy pochodną
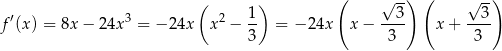
Widać teraz, że pochodna jest dodatnia dla 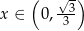 i ujemna dla
i ujemna dla 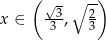 . To oznacza, że funkcja
. To oznacza, że funkcja 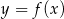 rośnie w przedziale
rośnie w przedziale 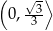 i maleje w przedziale
i maleje w przedziale 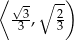 . W takim razie pole trójkąta
. W takim razie pole trójkąta 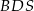 jest największe jeżeli
jest największe jeżeli 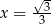 . Pozostało obliczyć objętość ostrosłupa w tym przypadku.
. Pozostało obliczyć objętość ostrosłupa w tym przypadku.
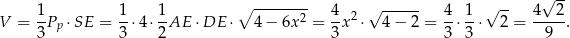
Odpowiedź: