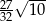/Szkoła średnia/Geometria/Stereometria/Zadania na ekstrema/Największe pole

Zadanie nr 9529382

Podstawą ostrosłupa 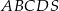ABCDS jest prostokąt o obwodzie 6. Krawędź 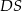DS jest wysokością ostrosłupa i jest 3 razy dłuższa od krawędzi 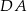DA . Jakie największe pole może mieć przekrój ostrosłupa płaszczyzną wyznaczoną przez wierzchołki 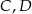C,D i środek krawędzi AS ?

Wersja PDF

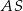Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

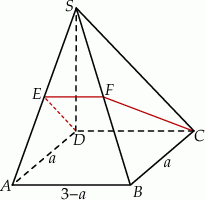
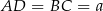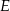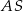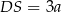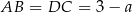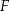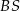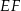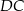Niech AD = BC = a oraz oznaczmy przez E środek krawędzi AS . Z założenia mamy wtedy DS = 3a i AB = DC = 3 − a . Zauważmy, że jeżeli F jest środkiem krawędzi BS , to odcinki EF i DC są oba równoległe do 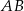AB , więc punkty 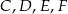C ,D ,E,F leżą w jednej płaszczyźnie i są wierzchołkami trapezu. W takim razie punkt 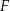F jest punktem, w którym płaszczyzna 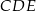CDE przecina krawędź BS .

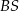Zauważmy ponadto, że krawędź 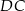DC jest prostopadła do płaszczyzny 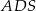ADS , więc jest prostopadła do prostej 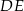DE leżącej w tej płaszczyźnie. To oznacza, że trapez 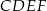CDEF jest trapezem prostokątnym i 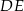DE jest jego wysokością. Z drugiej strony, 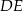DE jest środkową w trójkącie prostokątnym 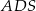ADS . Zauważmy, że przeciwprostokątna 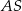AS tego trójkąta jest średnicą jego okręgu opisanego, zatem punkt 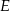E jest środkiem okręgu opisanego i

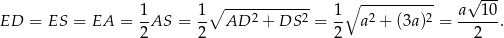
√ --- 1 1 ∘ ------------ 1 ∘ ----------- a 10 ED = ES = EA = -AS = -- AD 2 + DS 2 = -- a2 + (3a)2 = ------. 2 2 2 2

Możemy teraz obliczyć pole trapezu 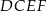DCEF .

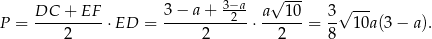
3−a- √ --- DC--+-EF-- 3−--a+---2-- a--1-0 3-√ --- P = 2 ⋅ED = 2 ⋅ 2 = 8 10a(3 − a).

Powyższe wyrażenie jest funkcją kwadratową zmiennej a , której wykres jest parabolą o ramionach skierowanych w dół. Największe pole przekroju otrzymamy więc w wierzchołku paraboli (dokładnie w środku między jej pierwiastkami), więc dla

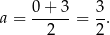
0+ 3 3 a = ------= -. 2 2

Pole przekroju jest wtedy równe

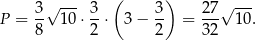
3 √ --- 3 ( 3) 27 √ --- P = -- 10⋅ --⋅ 3 − -- = --- 10. 8 2 2 32

 
Odpowiedź: √ --- 2372 10

Wersja PDF