/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny

Zadanie nr 4119096

Dodaj do ulubionych
Dodaj do rozwiązanych

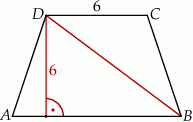
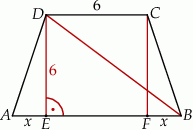
W trapezie równoramiennym 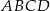ABCD krótsza podstawa 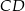CD ma długość równą 6 i jest równa wysokości trapezu. Długość dłuższej podstawy 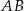AB jest równa długości przekątnej trapezu. Oblicz pole tego trapezu.

PIC

Rozwiązanie

Dorysujmy drugą wysokość trapezu i oznaczmy 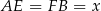AE = FB = x .

PIC

Piszemy twierdzenie Pitagorasa w trójkącie 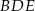BDE .

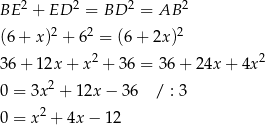
2 2 2 2 BE + ED = BD = AB (6+ x)2 + 62 = (6+ 2x)2 36+ 12x + x2 + 36 = 36+ 24x + 4x2 2 0 = 3x + 12x − 3 6 / : 3 0 = x2 + 4x − 12

Rozwiązujemy otrzymane równanie kwadratowe.

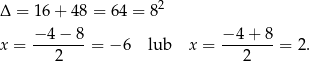
Δ = 16 + 4 8 = 64 = 8 2 x = −-4-−-8 = − 6 lub x = −-4-+-8 = 2. 2 2

Ujemne rozwiązanie odrzucamy i mamy 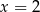x = 2 . Stąd 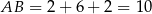AB = 2+ 6+ 2 = 10 i pole trapezu jest równe

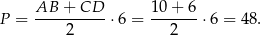
P = AB--+-CD--⋅6 = 10-+-6-⋅6 = 48. 2 2

 
Odpowiedź: 48

Wersja PDF