/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny

Zadanie nr 6776289

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie równoramiennym 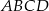ABCD ramię ma długość 13. Obwód tego trapezu jest równy 52. Wiedząc, że tangens kąta ostrego w trapezie 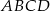ABCD jest równy 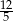125- , oblicz długości jego podstaw.

Rozwiązanie

Rozpoczynamy od rysunku.

PIC

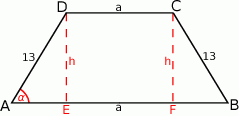
Sposób I

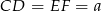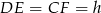Jeżeli oznaczymy CD = EF = a i DE = CF = h to z podanego tangensa mamy

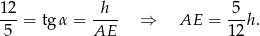
12 h 5 ---= tgα = ---- ⇒ AE = --h. 5 AE 12

Piszemy teraz twierdzenie Pitagorasa w trójkącie 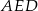AED .

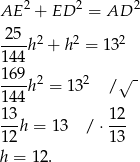
AE 2 + ED 2 = AD 2 25--2 2 2 144h + h = 13 169 √ - ---h2 = 132 / 144 13h = 1 3 / ⋅ 12- 12 13 h = 12.

Zatem

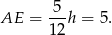
-5- AE = 12 h = 5.

Pozostało teraz skorzystać z podanego obwodu trapezu.

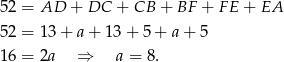
52 = AD + DC + CB + BF + F E + EA 52 = 13 + a + 13 + 5 + a + 5 16 = 2a ⇒ a = 8.

Zatem podstawy mają długość 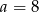a = 8 i

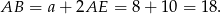
AB = a + 2AE = 8+ 10 = 18 .

Sposób II

Jeżeli oznaczymy 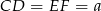CD = EF = a to z podanego obwodu mamy

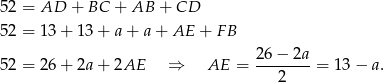
52 = AD + BC + AB + CD 52 = 13 + 13 + a + a + AE + F B 26− 2a 52 = 26 + 2a + 2AE ⇒ AE = --------= 1 3− a . 2

Z podanego tangensa mamy

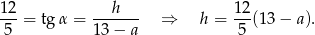
1 2 h 1 2 --- = tg α = ------- ⇒ h = ---(13 − a). 5 13 − a 5

Teraz pozostało napisać twierdzenie Pitagorasa w trójkącie 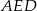AED .

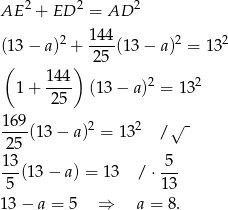
AE 2 + ED 2 = AD 2 2 1-44 2 2 (13 − a) + 25 (13 − a) = 1 3 ( 144) 1 + ---- (1 3− a )2 = 132 25 169- 2 2 √ - 25 (13 − a) = 1 3 / 13 5 --(13 − a) = 1 3 / ⋅--- 5 13 13 − a = 5 ⇒ a = 8.

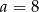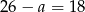Zatem podstawy mają długości a = 8 i 26− a = 18 .  
Odpowiedź: 8 i 18

Wersja PDF