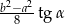/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Równoramienny

Zadanie nr 7152927

Dodaj do ulubionych
Dodaj do rozwiązanych

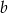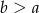W trapezie równoramiennym, którego podstawy mają długość a i b (b > a ), kąt ostry ma miarę α , połączono odcinkami środki sąsiednich boków. Oblicz pole powstałego czworokąta.

Rozwiązanie

Zaczynamy oczywiście od rysunku.

PIC

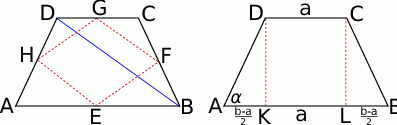
Sposób I

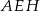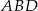Pokażemy, że pole otrzymanego czworokąta to dokładnie połowa pola trapezu. Rzeczywiście, trojkąty AEH i ABD są podobne w skali 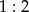1 : 2 , zatem

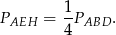
1 PAEH = -PABD . 4

Podobnie

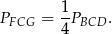
1 PFCG = -PBCD . 4

Zatem

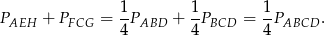
1- 1- 1- PAEH + PFCG = 4 PABD + 4PBCD = 4PABCD .

Podobnie pokazujemy, że

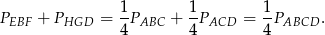
P + P = 1-P + 1P = 1P . EBF HGD 4 ABC 4 ACD 4 ABCD

Zatem

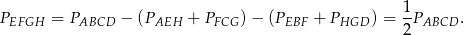
1 PEFGH = PABCD − (PAEH + PFCG )− (PEBF + PHGD ) = --PABCD . 2

Inny sposób zobaczenia, że 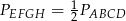PEFGH = 12PABCD to zauważyć, że czworokąt 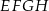EF GH jest rombem (długości jego boków to połowy długości przekątnych trapezu), oraz z tego, że 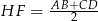HF = AB+CD-- 2 (własność odcinka łączącego środki ramion trapezu). Mamy zatem

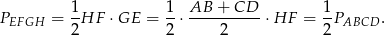
1 1 AB + CD 1 PEFGH = --HF ⋅GE = --⋅ ----------⋅HF = -PABCD . 2 2 2 2

Musimy zatem obliczyć pole trapezu. Znamy podstawy, a wysokość wyliczamy z trójkąta 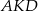AKD

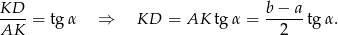
KD b − a ----= tgα ⇒ KD = AK tg α = ------tgα . AK 2

Zatem pole trapezu jest równe

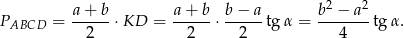
a + b a + b b − a b2 − a2 PABCD = ------⋅KD = ------⋅------tg α = -------tg α. 2 2 2 4

Pole czworokąta EF GH jest dwa razy mniejsze.

Sposób II

Widać, że utworzony czworokąt jest deltoidem (tak naprawdę jest rombem, ale deltoid nam wystarczy). Zatem jego pole jest równe połowie iloczynu długości przekątnych. Odcinek łączący środki ramion trapezu to średnia arytmetyczna jego podstaw, czyli 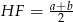a+b HF = -2-- . Wysokość wyliczamy jak w poprzednim sposobie (z trójkąta prostokątnego 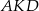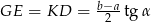AKD ) GE = KD = b−a-tg α 2 . Szukane pole jest więc równe

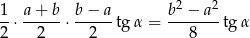
1 a + b b − a b2 − a2 --⋅------⋅------tgα = ------- tg α 2 2 2 8

 
Odpowiedź: b2−a2 8 tg α

Wersja PDF