/Szkoła średnia/Równania/Wykładnicze

Zadanie nr 2874990

Dodaj do ulubionych
Dodaj do rozwiązanych

Dla jakich wartości parametru 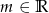m ∈ R równanie 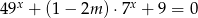x x 49 + (1 − 2m )⋅ 7 + 9 = 0 ma dwa różne rozwiązania?

Rozwiązanie

Podstawiając 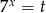x 7 = t mamy równanie

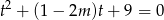
2 t + (1 − 2m )t+ 9 = 0

Jeżeli zapiszemy równość 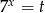x 7 = t w postaci

x log7 7 = log7 t ⇒ x = log7t,

to widać, że równanie będzie miało dwa rozwiązania jeżeli będą dwie dodatnie wartości 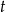t , czyli gdy równanie

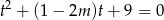
t2 + (1 − 2m )t+ 9 = 0

ma dwa pierwiastki dodatnie.

Na początek sprawdźmy kiedy to równanie kwadratowe ma dwa pierwiastki.

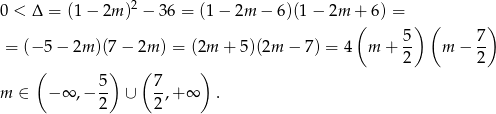
2 0 < Δ = (1− 2m ) − 36 = (1 − 2m − 6)(1− 2m +( 6) = ) ( ) 5 7 = (− 5− 2m )(7− 2m ) = (2m + 5)(2m − 7 ) = 4 m + 2- m − 2- ( ) ( ) 5- 7- m ∈ − ∞ ,− 2 ∪ 2,+ ∞ .

Pozostało ustalić kiedy pierwiastki są dodatnie. Tak będzie gdy ich suma i iloczyn są dodatnie, czyli na mocy wzorów Viéte’a

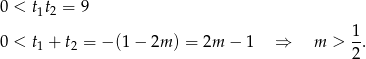
0 < t1t2 = 9 0 < t + t = − (1− 2m ) = 2m − 1 ⇒ m > 1. 1 2 2

W połączeniu z warunkiem na 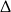Δ -ę mamy 7 m > 2 .  
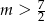Odpowiedź: m > 7 2

Wersja PDF