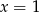/Szkoła średnia/Równania/Wykładnicze

Zadanie nr 4045159

Dodaj do ulubionych
Dodaj do rozwiązanych

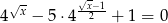Rozwiąż √x √x−1 4 − 5 ⋅4 2 + 1 = 0 .

Rozwiązanie

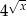Widać, że x w równaniu pojawia się w wyrażeniach typu √x 4 . Przekształcimy równanie, żeby dało się za coś w tym stylu podstawić.

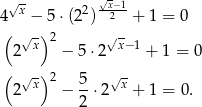
√ - √x−1 4 x − 5⋅(22) 2 + 1 = 0 ( √ -)2 √- 2 x − 5⋅ 2 x− 1 + 1 = 0 ( ) √x- 2 5- √x 2 − 2 ⋅2 + 1 = 0.

No i podstawiamy 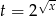√ - t = 2 x .

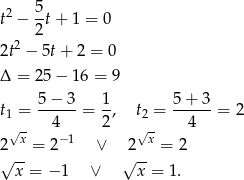
t2 − 5t + 1 = 0 2 2t2 − 5t+ 2 = 0 Δ = 25 − 16 = 9 5 − 3 1 5 + 3 t1 = ------= --, t2 = ------= 2 √x- 4− 1 2 √x- 4 2 = 2 ∨ 2 = 2 √x--= − 1 ∨ √x--= 1 .

Pierwsza równośc jest sprzeczna, a druga daje 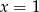x = 1 .  
Odpowiedź: x = 1

Wersja PDF