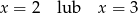/Szkoła średnia/Równania/Wykładnicze

Zadanie nr 4329764

Dodaj do ulubionych
Dodaj do rozwiązanych

Rozwiąż równanie 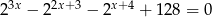3x 2x+3 x+4 2 − 2 − 2 + 128 = 0 .

Rozwiązanie

Jeżeli podstawimy 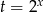x t = 2 , to równanie przyjmie postać

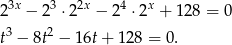
3x 3 2x 4 x 2 − 2 ⋅ 2 − 2 ⋅2 + 128 = 0 t3 − 8t2 − 16t + 12 8 = 0.

Sposób I

Rozkładamy otrzymany wielomian 3–stopnia grupując wyrazy.

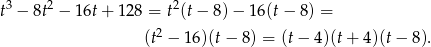
t3 − 8t2 − 16t+ 128 = t2(t− 8)− 16(t− 8 ) = (t2 − 16)(t− 8 ) = (t− 4)(t + 4)(t− 8).

Ujemne rozwiązanie odrzucamy i mamy

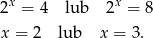
2x = 4 lub 2x = 8 x = 2 lub x = 3 .

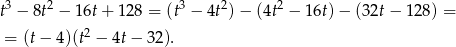
Sposób II

Szukamy pierwiastków całkowitych otrzymanego równania 3 stopnia wśród dzielników wyrazu wolnego. Próbując po kolei, znajdujemy pierwiastek 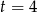t = 4 i dzielimy wielomian przez 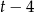t− 4 – my zrobimy to grupując wyrazy.

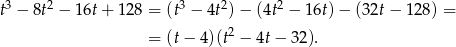
3 2 3 2 2 t − 8t − 16t + 128 = (t − 4t )− (4t − 1 6t)− (32t − 12 8) = 2 = (t− 4)(t − 4t− 32).

Rozkładamy teraz otrzymany trójmian

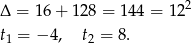
Δ = 16+ 128 = 14 4 = 122 t = − 4, t = 8. 1 2

Ujemne rozwiązanie odrzucamy (bo 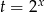x t = 2 ) i mamy

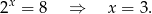
x 2 = 8 ⇒ x = 3.

Pamiętajmy jeszcze o rozwiązaniu 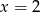x = 2 odpowiadającym t = 4 .  
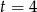Odpowiedź: x = 2 lub x = 3

Wersja PDF