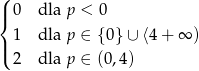Zadanie nr 4924794
Dane jest równanie 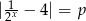 z parametrem
z parametrem 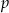 . Wyznacz liczbę rozwiązań tego równania w zależności od parametru
. Wyznacz liczbę rozwiązań tego równania w zależności od parametru 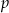 .
.
Rozwiązanie
Sposób I
W miarę łatwo jest narysować wykres lewej strony równania. Zaczynamy od 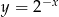 , potem przesuwamy go o 4 jednostki w dół i część pod osią
, potem przesuwamy go o 4 jednostki w dół i część pod osią 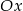 zaginamy do góry.
zaginamy do góry.
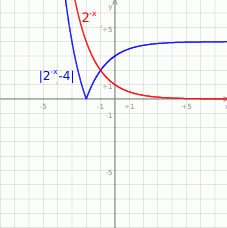
Z wykresu widać, że równanie nie ma rozwiązań dla 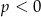 , ma dwa rozwiązania dla
, ma dwa rozwiązania dla 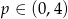 , i ma jedno rozwiązanie dla
, i ma jedno rozwiązanie dla 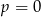 lub
lub 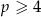 .
.
Sposób II
Zadanie możemy też rozwiązać algebraicznie. Równanie 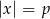 nie ma rozwiązań jeżeli
nie ma rozwiązań jeżeli 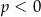 , ma jedno rozwiązanie
, ma jedno rozwiązanie 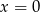 jeżeli
jeżeli 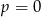 , i ma dwa rozwiązania
, i ma dwa rozwiązania 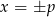 jeżeli
jeżeli 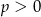 .
.
Zgodnie z powyższą uwagą, dane równanie nie ma rozwiązań dla 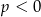 . Druga możliwość, to
. Druga możliwość, to  , czyli
, czyli
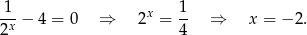
Mamy wtedy jedno rozwiązanie.
Ostatnia możliwość to 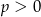 . Mamy wtedy
. Mamy wtedy 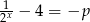 lub
lub 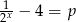 . To daje nam dwa rozwiązania chyba, że akurat któraś z tych równości jest sprzeczna. Jeżeli zapiszemy je w postaci
. To daje nam dwa rozwiązania chyba, że akurat któraś z tych równości jest sprzeczna. Jeżeli zapiszemy je w postaci
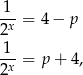
to widać, że drugie równanie będzie zawsze miało rozwiązanie (bo 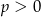 ). Pierwsze natomiast będzie miało rozwiązanie o ile
). Pierwsze natomiast będzie miało rozwiązanie o ile
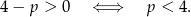
Zatem dla 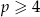 rozwiązanie jest tylko jedno.
rozwiązanie jest tylko jedno.
Odpowiedź: Liczba rozwiązań: