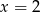Zadanie nr 7436172
Rozwiąż równanie 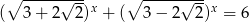 .
.
Rozwiązanie
Najważniejsze w tym zadaniu to zauważyć, że iloczyn liczb w nawiasach jest równy 1.
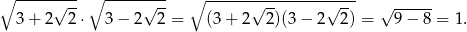
Jeżeli teraz podstawimy 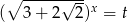 to mamy równanie
to mamy równanie
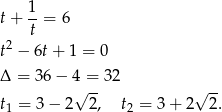
Daje to nam równania
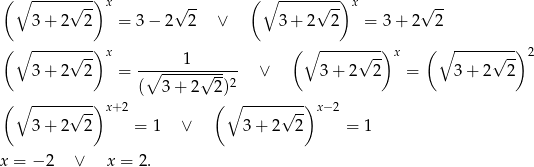
Odpowiedź: 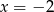 lub
lub 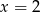
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Rozwiąż równanie 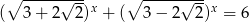 .
.
Najważniejsze w tym zadaniu to zauważyć, że iloczyn liczb w nawiasach jest równy 1.
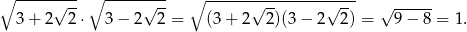
Jeżeli teraz podstawimy 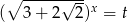 to mamy równanie
to mamy równanie
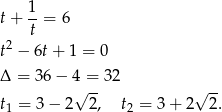
Daje to nam równania
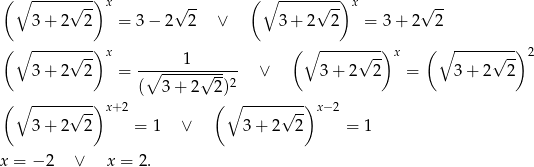
Odpowiedź: 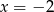 lub
lub