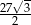Zadanie nr 8534376
W trapezie prostokątnym krótsza przekątna dzieli go na trójkąt prostokątny i trójkąt równoboczny. Dłuższa podstawa trapezu jest równa 6. Oblicz pole tego trapezu.
Rozwiązanie
Rozpoczynamy od rysunku.
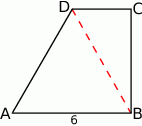
Zauważmy, że wysokość 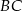 trapezu ma długość równą wysokości trójkąta równobocznego
trapezu ma długość równą wysokości trójkąta równobocznego 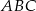 , czyli
, czyli
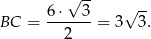
Długość podstawy 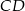 wyliczamy z twierdzenia Pitagorasa w trójkącie
wyliczamy z twierdzenia Pitagorasa w trójkącie 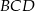 .
.
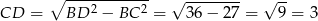
(mogliśmy też zauważyć, że 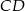 ma długość równą połowie długości podstawy
ma długość równą połowie długości podstawy 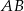 ).
).
Zatem pole trapezu jest równe
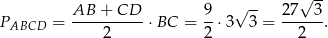
Odpowiedź: