/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny

Zadanie nr 2941191

Dodaj do ulubionych
Dodaj do rozwiązanych

Jeżeli skrócimy wysokość trapezu o polu 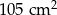2 1 05 cm o 2 cm i jednocześnie wydłużymy każdą z jego podstaw o 6 cm, to pole trapezu nie ulegnie zmianie. Wyznacz długość wysokości trapezu (przed zmianą).

Rozwiązanie

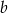Jeżeli oznaczymy długości podstaw trapezu przez a i b , a długość wysokości przez 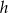h to mamy układ równań

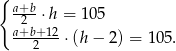
{ a+2b-⋅h = 105 a+b+12-⋅(h− 2) = 105 . 2

Podstawmy 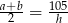a+b- 105 2 = h z pierwszego równania do drugiego.

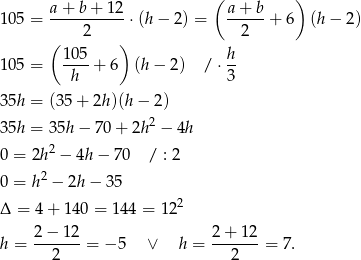
a + b + 12 ( a + b ) 10 5 = -----------⋅(h − 2) = ------+ 6 (h− 2) ( 2 ) 2 105- h- 10 5 = h + 6 (h− 2) / ⋅3 35h = (35 + 2h)(h − 2) 2 35h = 35h − 70 + 2h − 4h 0 = 2h2 − 4h− 70 / : 2 2 0 = h − 2h− 35 Δ = 4 + 140 = 144 = 122 h = 2−--12-= − 5 ∨ h = 2-+-12-= 7. 2 2

Ujemne rozwiązanie odrzucamy i mamy 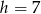h = 7 .  
Odpowiedź: 7 cm

Wersja PDF