/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez/Dowolny

Zadanie nr 2978355

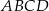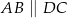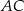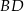W trapezie ABCD (AB ∥ DC ) przekątne AC i BD przecinają się w punkcie 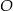O takim, że 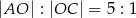|AO | : |OC | = 5 : 1 . Pole trójkąta 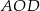AOD jest równe 10. Uzasadnij, że pole trapezu 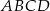ABCD jest równe 72.

PIC

Wersja PDF

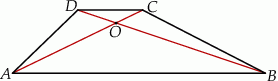
Rozwiązanie

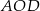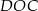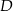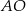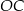Zauważmy, że trójkąty AOD i DOC mają wspólną wysokość opuszczoną z wierzchołka D , więc stosunek ich pól jest równy stosunkowi ich podstaw AO i OC . W takim razie

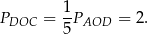
P = 1-P = 2 . DOC 5 AOD

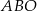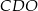Zauważmy teraz, że trójkąty ABO i CDO są podobne (bo mają równe kąty) oraz znamy ich skalę podobieństwa

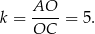
k = AO--= 5. OC

W takim razie pole trójkąta 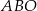ABO jest równe

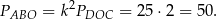
PABO = k2PDOC = 25 ⋅2 = 50.

Pozostało obliczyć pole trójkąta 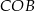COB . Można to zrobić na różne sposoby.

Sposób I

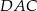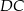Zauważmy, że trójkąty DAC i DBC mają wspólną podstawę DC oraz równe wysokości opuszczone na tę podstawę. W takim razie trójkąty te mają równe pola, co pozwala obliczyć pole trójkąta COB .

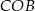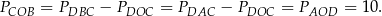
PCOB = PDBC − PDOC = PDAC − PDOC = PAOD = 10.

Pole trapezu jest więc równe

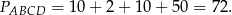
PABCD = 10+ 2+ 10+ 50 = 72.

Sposób II

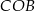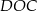Trójkąty COB i DOC mają wspólną wysokość opuszczoną z wierzchołka 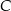C , więc stosunek ich pól jest równy stosunkowi ich podstaw: 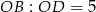OB : OD = 5 . Mamy zatem

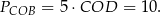
PCOB = 5 ⋅COD = 10 .

Pole całego trapezu liczymy tak samo jak w poprzednim sposobie.

Wersja PDF