Zadanie nr 7535531
Dany jest czworokąt 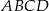 , w którym
, w którym 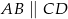 . Na boku
. Na boku 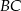 wybrano taki punkt
wybrano taki punkt 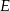 , że
, że 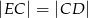 i
i 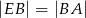 . Wykaż, że kąt
. Wykaż, że kąt 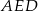 jest prosty.
jest prosty.
Rozwiązanie
Rozpoczynamy oczywiście od rysunku.
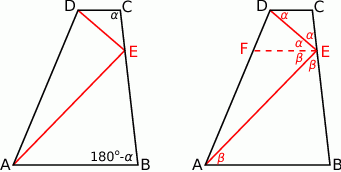
Sposób I
Oznaczmy 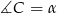 . Wtedy
. Wtedy 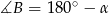 . Ponieważ każdy z trójkątów
. Ponieważ każdy z trójkątów 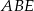 i
i 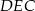 jest równoramienny mamy
jest równoramienny mamy
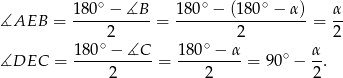
Zatem
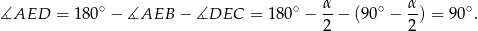
Sposób II
Tym razem oznaczmy 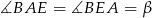 i
i 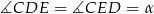 . Jeżeli dorysujemy odcinek
. Jeżeli dorysujemy odcinek 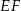 równoległy do podstaw trapezu, to mamy
równoległy do podstaw trapezu, to mamy
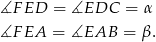
W szczególności