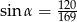Zadanie nr 3482753

Bok rombu ma długość 13, suma długości przekątnych jest równa 34.

Rozwiązanie

Zaczynamy od rysunku

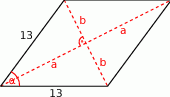
Przekątne w rombie dzielą się na połowy, więc

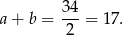
a + b = 34-= 17. 2

Zapiszmy układ równań wynikający z założeń

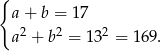
{ a+ b = 17 a2 + b 2 = 132 = 169 .

Sposób I

Zauważmy, że nie musimy wyznaczać i 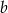, a jedynie pole rombu, czyli

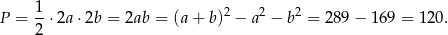
P = 1-⋅2a ⋅2b = 2ab = (a + b)2 − a2 − b2 = 289 − 169 = 120. 2

Sposób II

Z pierwszego równania układu wyznaczamy i podstawiamy do drugiego

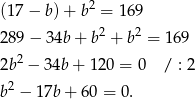
(17− b)+ b2 = 169 289− 34b + b2 + b2 = 169 2 2b − 34b+ 120 = 0 / : 2 b2 − 1 7b+ 60 = 0.

Liczymy wyróżnik i pierwiastki

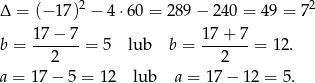
Δ = (− 17)2 − 4 ⋅60 = 28 9− 2 40 = 49 = 72 b = 17-−-7-= 5 lub b = 17-+-7-= 12. 2 2 a = 17− 5 = 12 lub a = 1 7− 12 = 5.

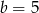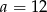Widzimy, że są to te same rozwiązania. My przyjmiemy b = 5 i a = 12 (żeby pozostać zgodnym z rysunkiem).

Mamy już obliczone połowy długości przekątnych, więc obliczenie pola powierzchni nie sprawi najmniejszych problemów – korzystamy ze wzoru z przekątnymi.
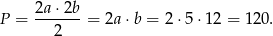
$2a⋅ 2b P = -------= 2a ⋅b = 2 ⋅5 ⋅12 = 12 0. 2$

Odpowiedź: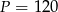
Sposób I

Korzystamy z poprzedniego podpunktu i ze wzoru na pole z sinusem.

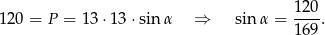
$120 12 0 = P = 13⋅ 13⋅sin α ⇒ sin α = ---. 169$

Sposób II

Tym razem skorzystamy z wyliczonych i 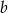oraz ze wzoru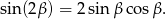

$sin(2β ) = 2sin βco sβ.$

Zatem

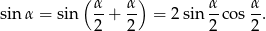
$(α α) α α sin α = sin --+ -- = 2sin --cos -. 2 2 2 2$

Teraz wystarczy już tylko podstawić odpowiednie wartości liczbowe

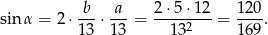
$sin α = 2 ⋅-b-⋅-a-= 2-⋅5-⋅12 = 120. 13 13 132 169$

Odpowiedź: