Zadanie nr 5020491
Bok rombu 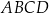 ma długość
ma długość  , a kąt ostry przy wierzchołku
, a kąt ostry przy wierzchołku 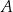 ma miarę
ma miarę 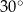 . Oblicz długość odcinka łączącego wierzchołek
. Oblicz długość odcinka łączącego wierzchołek 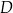 rombu z punktem boku
rombu z punktem boku 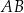 , dzielącego ten bok w stosunku
, dzielącego ten bok w stosunku 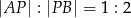 .
.
Rozwiązanie
Zacznijmy od rysunku i niech 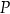 będzie punktem boku
będzie punktem boku 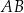 , o którym mowa w treści zadania.
, o którym mowa w treści zadania.

Ponieważ 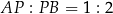 , to
, to
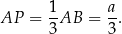
Długość odcinka 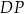 obliczamy z twierdzenia cosinusów.
obliczamy z twierdzenia cosinusów.
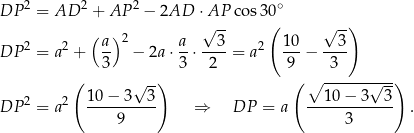
Odpowiedź: