/Szkoła średnia/Geometria/Planimetria/Czworokąt/Romb/Pole

Zadanie nr 7753597

Dodaj do ulubionych
Dodaj do rozwiązanych

Jeżeli skrócimy dłuższą przekątną rombu przy każdym wierzchołku o 4 cm, zaś przedłużymy krótszą przekątną o 1 cm, to otrzymamy kwadrat. Pole otrzymanego kwadratu jest o 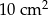1 0 cm 2 mniejsze od pola rombu. Oblicz pole rombu i pole kwadratu.

Rozwiązanie

Możemy zacząć od schematycznego obrazka.

PIC

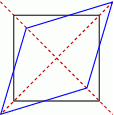
Jeżeli oznaczymy długości przekątnych rombu przez 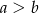a > b , to ze wzoru na pole rombu z przekątnymi, mamy

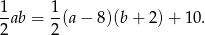
1ab = 1(a − 8)(b + 2) + 10 . 2 2

Z lewej strony mamy pole rombu, a z prawej pole kwadratu z uwzględnieniem brakującej 10. Przekształcając mamy

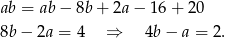
ab = ab − 8b + 2a − 16 + 20 8b− 2a = 4 ⇒ 4b − a = 2.

Co dalej? - musimy jeszcze skorzystać z tego, że zmieniając przekątne dostaliśmy kwadrat, czyli

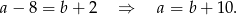
a− 8 = b + 2 ⇒ a = b + 10 .

Wstawiając to do poprzedniego równania mamy

4b − b − 10 = 2 ⇒ 3b = 12 ⇒ b = 4.

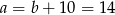Zatem a = b + 10 = 14 i pole rombu jest równe

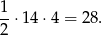
1 --⋅14 ⋅4 = 28 . 2

Pole kwadratu jest o 10 mniejsze.  
Odpowiedź: 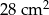2 28 cm i 2 18 cm

Wersja PDF