Zadanie nr 2888765

Oblicz sumę szóstych potęg pierwiastków równania 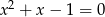2 x + x − 1 = 0 .

Rozwiązanie

Na mocy wzorów Viète’a pierwiastki 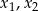x 1,x2 danego równania spełniają

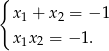
{ x1 + x2 = − 1 x1x 2 = − 1.

Sposób I

Obliczamy na rozgrzewkę sumę sześcianów pierwiastków

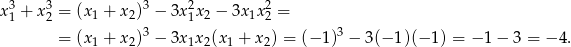
x31 + x32 = (x1 + x2)3 − 3x12x 2 − 3x 1x22 = 3 3 = (x1 + x2) − 3x1x 2(x1 + x2) = (− 1) − 3(− 1)(− 1) = − 1 − 3 = − 4.

Teraz liczymy sumę szóstych potęg.

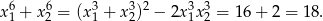
x6+ x6 = (x3 + x3)2 − 2x 3x 3= 16 + 2 = 18 . 1 2 1 2 1 2

Sposób II

Tym razem na początek obliczamy sumę kwadratów pierwiastków

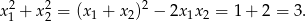
2 2 2 x1 + x2 = (x 1 + x 2) − 2x 1x2 = 1 + 2 = 3.

Teraz obliczamy sumę szóstych potęg – korzystamy ze wzoru na sumę sześcianów

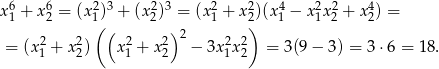
6 6 2 3 2 3 2 2 4 2 2 4 x1 + x2 = (x 1() + (x2) = (x1 + x2))(x1 − x1x2 + x2) = 2 2 ( 2 2)2 2 2 = (x1 + x2) x1 + x2 − 3x 1x2 = 3(9− 3) = 3 ⋅6 = 18.

Odpowiedź: 18