Zadanie nr 4473013
Wyznacz wszystkie liczby 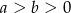 takie, że
takie, że 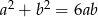 .
.
Rozwiązanie
Przekształcamy równanie
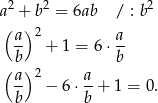
Podstawiamy teraz 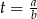 .
.
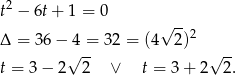
Ponieważ 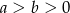 mamy
mamy
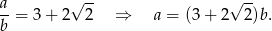
Odpowiedź: 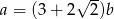 i
i 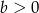 dowolne
dowolne
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyznacz wszystkie liczby 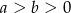 takie, że
takie, że 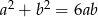 .
.
Przekształcamy równanie
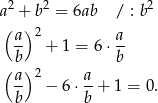
Podstawiamy teraz 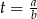 .
.
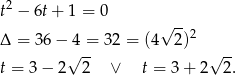
Ponieważ 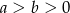 mamy
mamy
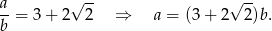
Odpowiedź: 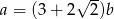 i
i 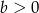 dowolne
dowolne
